
| 5 |
| x |
| AB |
| AC |
| 5 |
| a |
| 5 |
| b |
| AB |
| AC |
| AB |
| AC |
| 5 |
| x |
| AB |
| AC |
| 20 |
| 9k2 |
| 5 |
| k |
| 4 |
| 9 |
| 4 |
| 9 |

| 5 |
| a |
| AB |
| AC |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 5 |
| b |
| AB |
| AC |
| AC |
| BC |
| 1 |
| 6 |
| b |
| b-x1 |
| 1 |
| 6 |
| 5 |
| x1 |
| 1 |
| b |
| 1 |
| b |
| 1 |
| b |
| 5 |
| x |
| 4 |
| k |
| 5 |
| k |
| AB |
| AC |
| 4 |
| k |
| 2 |
| 3k |
| 20 |
| 9k2 |
| 5 |
| k |
| 4 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
| 4 |
| 9 |
| AB |
| AC |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
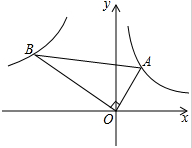 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=| 1 |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
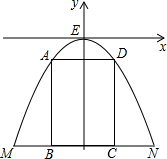 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.查看答案和解析>>
科目:初中数学 来源: 题型:
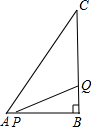 如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com