
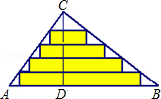
 如图,△ABC是一张直角三角形彩色纸,∠ACB=90°,AC=30cm,BC=40cm,CD⊥AB于点D.
如图,△ABC是一张直角三角形彩色纸,∠ACB=90°,AC=30cm,BC=40cm,CD⊥AB于点D.分析 (1)先利用勾股定理计算出AB=50cm,再利用面积法可计算出CD=24cm;
(2)如图,先证明△CEF∽△CAB,由于斜边上的高CD被五等分,所以$\frac{EF}{AB}$=$\frac{CK}{CD}$=$\frac{1}{5}$则EF=$\frac{1}{5}$×50=10,同理可得MN=$\frac{2}{5}$AB=20,PQ=$\frac{3}{5}$AB=30,GH=$\frac{4}{5}$AB=40,然后根据矩形的面积公式计算.
解答 解:(1)∵∠ACB=90°,AC=30cm,BC=40cm,
∴AB=$\sqrt{3{0}^{2}+4{0}^{2}}$=50(cm),
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=$\frac{30×40}{50}$=24(cm);
(2)如图,∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{EF}{AB}$=$\frac{CK}{CD}$=$\frac{1}{5}$,
∴EF=$\frac{1}{5}$×50=10,
同样方法可得MN=$\frac{2}{5}$AB=20,
PQ=$\frac{3}{5}$AB=30,
GH=$\frac{4}{5}$AB=40,
∴这4张纸条的面积和=10×$\frac{24}{5}$+20×$\frac{24}{5}$+30×$\frac{24}{5}$+40×$\frac{24}{5}$=480(cm2).
故答案为24cm,480cm2.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,然后利用三角形相似,对应边成比例计算相应线段的长.


科目:初中数学 来源: 题型:解答题
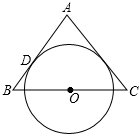 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
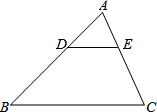 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (+3)-|-3| | B. | |+3|+|-3| | C. | (-3)-3 | D. | $\frac{2}{3}+$(-$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com