
 如图,长方形ABCD中,AB=10,BC=5,在CD上是否存在点P,使∠APB=90°?试说明理由.
如图,长方形ABCD中,AB=10,BC=5,在CD上是否存在点P,使∠APB=90°?试说明理由.| DP |
| BC |
| AD |
| PC |
 解:存在点P,使∠APB=90°;理由如下:
解:存在点P,使∠APB=90°;理由如下:| DP |
| BC |
| AD |
| PC |
| λ |
| 5 |
| 5 |
| 10-λ |


科目:初中数学 来源: 题型:
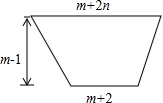 如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.
如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.查看答案和解析>>
科目:初中数学 来源: 题型:
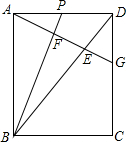 如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.| DE |
| BE |
| DE |
| BE |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、AB=A′B′ |
| B、AB一定平行于A′B′ |
| C、∠B=∠B′ |
| D、△ABC≌△A′B′C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间t(s) | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度h(m) | 4.9×1 | 4.9×4 | 4.9×9 | 4.9×16 | 4.9×25 | 4.9×36 |
查看答案和解析>>
科目:初中数学 来源: 题型:
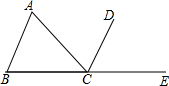 如图所示,在△ABC中,以C为顶点,在△ABC外作∠ACD=∠A,且点A和点D在直线BC的同侧,延长BC至E,在所作的图形中:
如图所示,在△ABC中,以C为顶点,在△ABC外作∠ACD=∠A,且点A和点D在直线BC的同侧,延长BC至E,在所作的图形中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com