
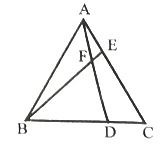
【题目】如图,已知![]() 为等边三角形,点D、E分别在BC、AC边上,且
为等边三角形,点D、E分别在BC、AC边上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)120°.
【解析】
(1)根据等边三角形的性质可知∠BAC=∠C=60°,AB=CA,结合AE=CD,可证明△ABE≌△CAD(SAS);
(2)根据∠AFB=180°-(∠ABE+∠BAD),∠ABE=∠CAD,可知∠AFB=180°-(∠CAD+∠BAD)=180°-60°=120°.
(1)∵△ABC为等边三角形,∴∠BAE=∠C=60°,AB=CA,
在△ABE和△CAD中,
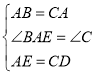 ,∴△ABE
,∴△ABE![]() △CAD(SAS).
△CAD(SAS).
(2)∵在△ABC中,∠AFB=180°-(∠ABE+∠BAD),
又∵△ABE![]() △CAD,∴∠ABE=∠CAD,∴∠AFB=180°-(∠ABE+∠BAD)=180°-(∠CAD+∠BAD)=180°-60°=120°.
△CAD,∴∠ABE=∠CAD,∴∠AFB=180°-(∠ABE+∠BAD)=180°-(∠CAD+∠BAD)=180°-60°=120°.


科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,然后改为步行,到达图书馆恰好用45min:小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示.
(1)家与图书馆之间的路程为 m,小东从图书馆到家所用的时间为 .
(2)求小玲步行时y与x之间的函数关系式.
(3)求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
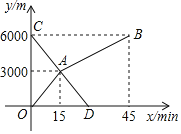
已知:如图,∠BAC.求作:∠BAC的角平分线AP.
小霞的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
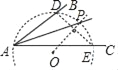
所以射线AP为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() ,
,![]() ,
,![]() 垂足为A,B,
垂足为A,B,![]() ,点
,点![]() 在线段
在线段![]() 上以每秒2
上以每秒2![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.它们运动的时间为
运动.它们运动的时间为![]() (
(![]() ).
).
(1)![]()
![]() ,
,![]()
![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(2)如点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,并判断此时线段
是否全等,并判断此时线段![]() 和线段
和线段![]() 的位置关系,请分别说明理由;
的位置关系,请分别说明理由;
(3)如图(2),将图(1)中的“![]() ,
,![]() ”,改为“
”,改为“![]() ”,其他条件不变.设点
”,其他条件不变.设点![]() 的运动速度为
的运动速度为![]()
![]() ,是否存在有理数
,是否存在有理数![]() ,
,![]() 与
与![]() 是否全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
是否全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
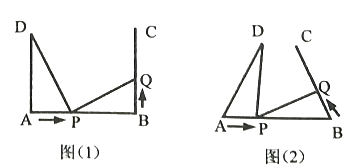
查看答案和解析>>
科目:初中数学 来源: 题型:
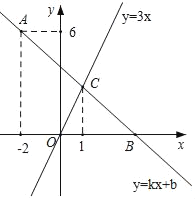
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州某游乐园门票价格为每人100元,20人以上(含20人)的团体票8折优惠.
(1)建兰中学初二年级一等奖学金获得者共有18人,学校奖励他们去游玩,你认为学校买18张门票,还是多买2张(买20张)购团体票更合算?
(2)如果获奖的学生不足20人,那么人数达到多少人时购买团体票比买普通票更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
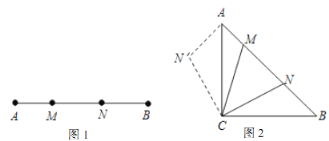
【题目】定义:如(图1),点![]() 把线段
把线段![]() 分割成
分割成![]() 和
和![]() ,若以
,若以![]() 为边的三角形是一个直角三角形,则称点
为边的三角形是一个直角三角形,则称点![]() 是线段
是线段![]() 的勾股分割点.
的勾股分割点.
(1)已知点![]() 是线段
是线段![]() 的勾股分割点,若
的勾股分割点,若![]() ,求
,求![]() 的长;
的长;
(2)如(图2),在等腰直角![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上两点,满足
上两点,满足![]() ,求证:点
,求证:点![]() 是线段
是线段![]() 的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把
的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 试一试.请根据陈老师的提示完成第(2)小题的证明过程.
试一试.请根据陈老师的提示完成第(2)小题的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com