
【题目】抛物线y1=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. 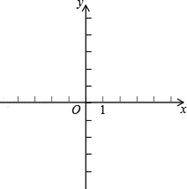
(1)求这条抛物线的表达式;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,若点C在直线y2=﹣3x+t上,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求n的取值范围.
【答案】
(1)解:∵抛物线与y轴交于点C,
∴C(0,﹣3).
∵抛物线与x轴交于A、B两点,OB=OC,
∴B(3,0)或B(﹣3,0).
∵点A在点B的左侧,m>0,
∴抛物线经过点B(3,0).
∴0=9m+3(m﹣3)﹣3.
∴m=1.
∴抛物线的表达式为y1=x2﹣2x﹣3
(2)解:由(1)可知:y1=x2﹣2x﹣3=(x﹣1)2﹣4,
∵点C在直线y2=﹣3x+t上,
∴t=﹣3,
∴y2=﹣3x﹣3,
y1向左平移n个单位后,则表达式为:y3=(x﹣1+n)2﹣4,
则当x≥1﹣n时,y随x增大而增大,
y2向下平移n个单位后,则表达式为:y4=﹣3x﹣3﹣n,
要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4,
即(1﹣n﹣1+n)2﹣4≤﹣3(1﹣n)﹣3﹣n,
解得:n≥1
【解析】(1)由抛物线的解析式易求点C的坐标,进而可求出点B的坐标,把点B的坐标代入抛物线的解析式可求出m的值,则抛物线的解析式也可求出;(2)由点C在直线y2=﹣3x+t上,可知t=﹣3,若y1向左平移n个单位后,则表达式为:y3=(x﹣1+n)2﹣4,若y2向下平移n个单位后,则表达式为:y4=﹣3x﹣3﹣n,要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4 , 进而可求出n的取值范围.
【考点精析】根据题目的已知条件,利用二次函数图象的平移和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 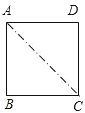

A.0.5cm
B.1cm
C.1.5cm
D.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65 岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化.从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果.所谓“老年人口抚养比”是指某范围人口中,老年人口数(65 岁及以上人口数)与劳动年龄人口数(15﹣64 岁人口数)之比,通常用百分比表示,用以表明每100 名劳动年龄人口要负担多少名老年人.
以下是根据我国近几年的人口相关数据制作的统计图和统计表.
2011﹣2014 年全国人口年龄分布图
2011﹣2014 年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0﹣14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15﹣64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
根据以上材料解答下列问题:
(1)2011 年末,我国总人口约为亿,全国人口年龄分布表中m的值为;
(2)若按目前我国的人口自然增长率推测,到2027 年末我国约有14.60 亿人.假设0﹣14岁人口占总人口的百分比一直稳定在16.5%,15﹣64岁人口一直稳定在10 亿,那么2027 年末我国0﹣14岁人口约为亿,“老年人口抚养比”约为;(精确到1%)
(3)2016 年1 月1 日起我国开始实施“全面二胎”政策,一对夫妻可生育两个孩子,在未来10年内,假设出生率显著提高,这(填“会”或“不会”)对我国的“老年人口抚养比”产生影响.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
(1)小文认为菱形是特殊的“筝形”,你认为他的判断正确吗?
(2)小文根据学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程,请补充完成:
①他首先发现了这类“筝形”有一组对角相等,并进行了证明,请你完成小文的证明过程.
已知:如图,在”筝形”ABCD中,AB=AD,CB=CD.
求证:∠ABC=∠ADC.
证明:②小文由①得到了这类“筝形”角的性质,他进一步探究发现这类“筝形”还具有其它性质,请再写出这类“筝形”的一条性质(除“筝形”的定义外);
③继性质探究后,小文探究了这类“筝形”的判定方法,写出这类“筝形”的一条判定方法(除“筝形”的定义外):
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC上一点,联结BD,∠CBD=∠A. 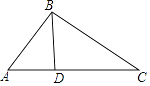
(1)求证:△CBD∽△CAB;
(2)若D是AC中点,CD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】里约奥运会后,受到奥运健儿的感召,群众参与体育运动的热度不减,全民健身再次成为了一种时尚,球场上也出现了更多年轻人的身影.请问下面四幅球类的平面图案中,是中心对称图形的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601, ![]() ≈1.414].
≈1.414].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC. 
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧 ![]() 的长l.
的长l.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com