
【题目】如图,等边三角形![]() 中,
中,![]() 是
是![]() 边的中点,
边的中点,![]() 是射线
是射线![]() 上一点,以
上一点,以![]() 为边作
为边作![]() ,使得
,使得![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
【答案】![]()
【解析】
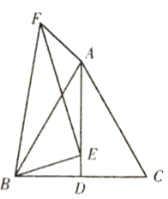
如下图,利用∠FEB=90°,可推导出△BED∽△EFG,设DE=x,根据![]() 和等边△ABC的边长为2,可得BD=1,GE=2,FG=2x,从而可用x表示出GA的长,在Rt△FGA中,利用勾股定理可求得用x表示的FA的长,最后利用二次函数性质,求得最小值
和等边△ABC的边长为2,可得BD=1,GE=2,FG=2x,从而可用x表示出GA的长,在Rt△FGA中,利用勾股定理可求得用x表示的FA的长,最后利用二次函数性质,求得最小值
图下图,过点F作AD的垂线,交AD的方向延长线于点G.

∵∠BEF=90°
∴∠BED+∠FEG=90°
∵△ABC是正三角形,点D是BC中点,AB=2
∴∠BDA=90°,BD=1,AD=![]()
∴∠EBD+∠BED=90°
∴∠EBD=∠FEG
∵∠BDE=∠FGE=90°
∴△BED∽△EFG
∵![]() ,∴
,∴![]()
∴![]()
∴EG=2
设DE=x,则AE=![]() ,GA=GE-AE=2+x-
,GA=GE-AE=2+x-![]() ,FG=2x
,FG=2x
∴在Rt△AFG中,![]()
化简得:![]()
要使AF最短,则只需要![]() 最小即可,即
最小即可,即![]() 最小
最小
令y=![]() ,则只需要求解二次函数的最小值即可
,则只需要求解二次函数的最小值即可
抛物线开口向上,顶点处即为最小值
此刻,![]() ,
,
∴结合二次函数的性质可得,
y=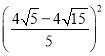
故AF的最小值为:![]()
故答案为:![]()


科目:初中数学 来源: 题型:
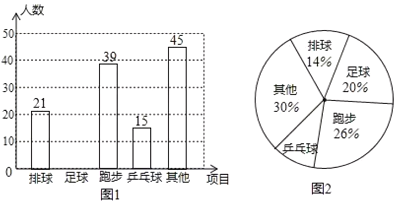
【题目】某校开展“我最喜欢的一项体育社团活动”调查,若每名学生必选且只能选一项,现随机抽查了![]() 名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
(1)求![]() 的值;
的值;
(2)补全条形统计图;
(3)求“乒乓球”所对应的扇形圆心角的度数;
(4)已知该校共有2400名学生,请你估计该校学生最喜欢篮球社团活动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
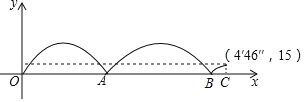
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑的最快的一位选手与最慢的一位选手的跑步过程(最快的选手跑完了全程),其中x表示最快的选手的跑步时间,y表示这两位选手之间的距离,现有以下4种说法,正确的有( )
①最快的选手到达终点时,最慢的选手还有15米未跑;
②跑的最快的选手用时4'46″;
③出发后最快的选手与最慢的选手相遇了两次;
④出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时长.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将抛物线![]() 向右平移
向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,得到抛物线
个单位,得到抛物线![]() ,直线
,直线![]() 与
与![]() 的一个交点记为
的一个交点记为![]() ,与
,与![]() 的一个交点记为
的一个交点记为![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 在第一象限内.
在第一象限内.
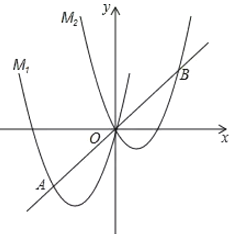
(1)求点![]() 的坐标及
的坐标及![]() 的表达式;
的表达式;
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,在
,在![]() 的右侧作正方形
的右侧作正方形![]() .
.
①当点![]() 的横坐标为
的横坐标为![]() 时,直线
时,直线![]() 恰好经过正方形
恰好经过正方形![]() 的顶点
的顶点![]() ,求此时
,求此时![]() 的值;
的值;
②在点![]() 的运动过程中,若直线
的运动过程中,若直线![]() 与正方形
与正方形![]() 始终没有公共点,直接写出
始终没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟影响,2019 年肉价大幅.上涨.某养殖场与2018年相比,生猪出栏数减少![]() 头.平均每头出栏价是2018年的
头.平均每头出栏价是2018年的![]() 倍,销售总额比2018年增加
倍,销售总额比2018年增加![]() .
.
![]() 若养殖场2018年生猪销售额为
若养殖场2018年生猪销售额为![]() 万元,求2019年平均每头生猪的出栏价格.
万元,求2019年平均每头生猪的出栏价格.
![]() 一猪肉专营店在5月份经营中,售价为
一猪肉专营店在5月份经营中,售价为![]() 元
元![]() 天可卖
天可卖![]() .6月份每千克上涨
.6月份每千克上涨![]() 元,则
元,则![]() 天少卖
天少卖![]() .受产业链影响继续涨价,销量继续递减.若猪肉的成本折算为
.受产业链影响继续涨价,销量继续递减.若猪肉的成本折算为![]() 元
元![]() 专营店平均每天规划毛利约
专营店平均每天规划毛利约![]() 元,求这家专营店
元,求这家专营店![]() 天为养殖场赚的最大毛利.
天为养殖场赚的最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春临大地,学校决定给长12米,宽9米的一块长方形展示区进行种植改造现将其划分成如图两个区域:区域Ⅰ矩形ABCD部分和区域Ⅱ四周环形部分,其中区域Ⅰ用甲、乙、丙三种花卉种植,且EF平分BD,G,H分别为AB,CD中点.
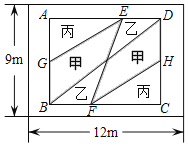
(1)若区域Ⅰ的面积为Sm2,种植均价为180元/m2,区域Ⅱ的草坪均价为40元/m2,且两区域的总价为16500元,求S的值.
(2)若AB:BC=4:5,区域Ⅱ左右两侧草坪环宽相等,均为上、下草坪环宽的2倍
①求AB,BC的长;
②若甲、丙单价和为360元/m2,乙、丙单价比为13:12,三种花卉单价均为20的整数倍.当矩形ABCD中花卉的种植总价为14520元时,求种植乙花卉的总价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
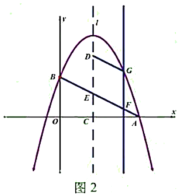
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com