
【题目】如图.PA和PB分别与⊙O相切于A,B两点,作直径AC,并延长交PB于点D.连结OP,CB.
(1)求证:OP∥CB;
(2)若PA=12,DB:DC=2:1,求⊙O的半径.

科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选择:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):

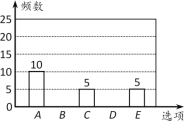
根据以上信息解答下列问题:
⑴ 这次被调查的学生有多少人?
⑵ 表中m的值为 ,并补全条形统计图;
⑶若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(2,0),交
轴交于点A(2,0),交![]() 轴于点B(0,
轴于点B(0,![]() ),直线
),直线![]() 过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
⑴填空:![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
⑵探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶设△PMN的周长为![]() ,点P的横坐标为x,求
,点P的横坐标为x,求![]() 与x的函数关系式,并求出
与x的函数关系式,并求出![]() 的最大值.
的最大值.
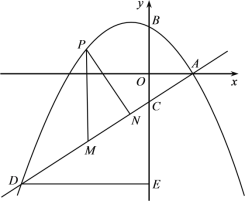
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
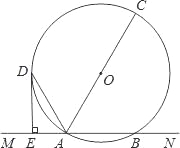
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
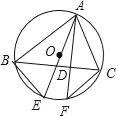
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
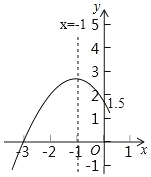
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示.
(1)确定二次函数的解析式;
(2)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com