
分析 首先由根与系数的关系得出两个根的和与积,再把所求式子通分,然后运用完全平方公式,代入两个根的和与积计算即可.
解答 解:∵x1,x2是方程2x2+5x-4=0的两个实数根,
∴x1+x2=-$\frac{5}{2}$,x1•x2=-2,
∴$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\frac{25}{4}+4}{-2}$=-$\frac{41}{8}$.
点评 此题主要考查了一元二次方程根与系数的关系,根据题意得出x1+x2=-$\frac{b}{a}$和x1•x2=$\frac{c}{a}$的值是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
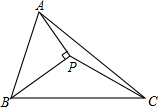 如图,在△ABC中,AP垂直∠B的平分线BP于P.若△PBC的面积为12cm2,且△APB的面积是△APC的面积的2倍.则△APB的面积=8cm2.
如图,在△ABC中,AP垂直∠B的平分线BP于P.若△PBC的面积为12cm2,且△APB的面积是△APC的面积的2倍.则△APB的面积=8cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x+3 | B. | y=2x-3 | C. | y=3x-3 | D. | y=4x-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示:AD平分∠BAC交BC于D,写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论.
如图所示:AD平分∠BAC交BC于D,写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
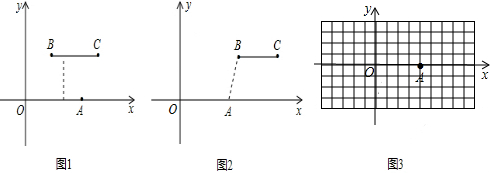
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com