
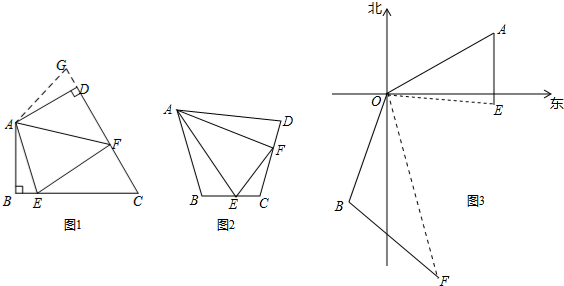
分析 问题背景:延长FD到点G,使DG=BE,连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
探索延伸:将△ADF顺时针旋转得到△ABG,使得AD与AB重合,则△ADF≌△ABG,即可证明△ABE≌△ADG,可得EF=FG,即可解题;
结论应用:连接EF,根据(2)的结论可证.
解答 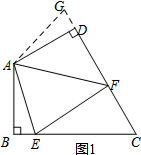 解:问题背景:EF=BE+DF,证明如下:
解:问题背景:EF=BE+DF,证明如下:
如图1,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF;
探索延伸:
证明:如图2,将△ADF顺时针旋转得到△ABG,使得AD与AB重合,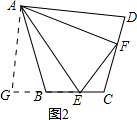 则△ADF≌△ABG,
则△ADF≌△ABG,
∴∠FAG=∠BAD,AF=AG,DF=GB,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
$\left\{\begin{array}{l}{AG=AF}\\{∠EAF=∠EAG}\\{AE=AE}\end{array}\right.$,
∴△EAG≌△EAF,(SAS)
∴GE=EF,
∵GE=GB+BE=DF+BE,
∴EF=BE+FD;
结论应用:如图3,连接EF,
∵∠AOB=30°+90°+20°=140°,
∴∠FOE=70°=$\frac{1}{2}$∠AOB,
又∵OA=OB,∠A+∠B=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE++FB=2×40+2×50=180(海里)
答:此时两舰艇之间的距离为180海里.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEF≌△AGF是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
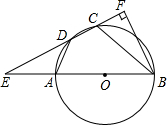 已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.
已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
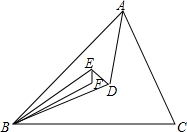 如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 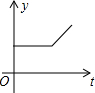 | B. | 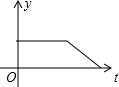 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6.-3) | B. | (-3,6) | C. | (6,3) | D. | (3,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com