Question

14．如图①，在平面直角坐标系中，点A的坐标为（1，-2），点B的坐标为（3，-1），二次函数y=-x²的图象为l₁
（1）平移抛物线l₁，使平移后的抛物线经过A，B两点，所得的抛物线为l₂，如图②，求抛物线l₂的解析式及顶点C的坐标，并求△ABC的面积；
（2）在y轴上是否存在点P，使S_△ABC=S_△ABP？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）利用待定系数法即可求得函数的解析式，过点A、B、C三点分别作x轴的垂线，垂足分别为D、E、F，求得△ABC的面积，；
（2）分当点P位于点G的下方和上方两种情况进行讨论求解．

解答 解：（1）设平移后的函数解析式为y=-（x-h）²+k，
∵平移后的抛物线经过A，B两点，
∴把A（1，-2），B（3，-1）代入得
$\left\{\begin{array}{l}{-（1-h）^{2}+k=-2}\\{-（3-h）^{2}+k=-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{h=\frac{9}{4}}\\{k=-\frac{7}{16}}\end{array}\right.$，
∴抛物线l₂的解析式为y=-（x-$\frac{9}{4}$）²-$\frac{7}{16}$，
∴顶点C（$\frac{9}{4}$，-$\frac{7}{16}$），
过点A、B、C三点分别作x轴的垂线，垂足分别为D、E、F，则AD=2，CF=$\frac{7}{16}$，BE=1，DE=2，DF=$\frac{5}{4}$，FE=$\frac{3}{4}$．
得：S_△ABC=S_梯形ABED-S_梯形BCFE-S_梯形ACFD=$\frac{15}{16}$．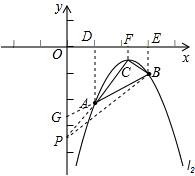

（2）存在，
延长BA交y轴于点G，直线AB的解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$，则点G的坐标为（0，-$\frac{5}{2}$），设点P的坐标为（0，h）
①当点P位于点G的下方时，PG=-$\frac{5}{2}$-h，连结AP、BP，则S_△APG=S_△BPG-S_△ABP=-$\frac{5}{2}$-h，
又∵S_△ABC=S_△ABP=$\frac{15}{16}$，得h=-$\frac{55}{16}$，点P的坐标为（0，-$\frac{55}{16}$）．
②当点P位于点G的上方时，PG=$\frac{5}{2}$+h，同理得h=-$\frac{25}{16}$，点P的坐标为（0，-$\frac{25}{16}$）．
综上所述所求点P的坐标为（0，-$\frac{55}{16}$）或（0，-$\frac{25}{16}$）．

点评 本题是待定系数法求函数的解析式，以及函数的平移的综合题，正确理解平移时，函数解析式的变化规律是关键．