
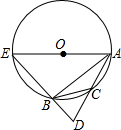
 如图,已知在⊙O中,点C为弧AB的中点,连接AC并延长至D,使CD=CA,连接DB并延长交⊙O于点E,连接AE.若AE=13,AC=5,则AB=
如图,已知在⊙O中,点C为弧AB的中点,连接AC并延长至D,使CD=CA,连接DB并延长交⊙O于点E,连接AE.若AE=13,AC=5,则AB= |
| AC |
 |
| BC |
| 50 |
| 13 |
102-(
|
| 120 |
| 13 |
| 120 |
| 13 |


科目:初中数学 来源: 题型:
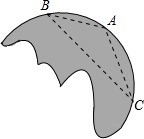 一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;
一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
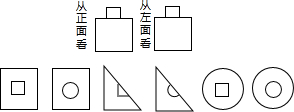 如图所示是一个几何体的从正面和左面看的图形,某班同学在探究它的从上面看的图形时,画出了如下图所示的几个图形,其中可能是该几何体从上面看的图形有( )
如图所示是一个几何体的从正面和左面看的图形,某班同学在探究它的从上面看的图形时,画出了如下图所示的几个图形,其中可能是该几何体从上面看的图形有( )| A、3个 | B、4个 | C、5个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°,请你猜想直线EF与CD有怎样的位置关系,并说明理由.
如图,在△ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°,请你猜想直线EF与CD有怎样的位置关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com