
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
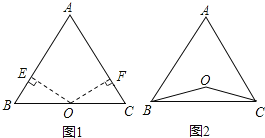
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
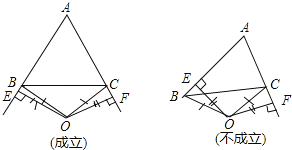
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
试题分析:(1)求证AB=AC,就是求证∠B=∠C,可通过构建全等三角形来求.过点O分别作OE⊥AB于E,OF⊥AC于F,那么可以用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC来实现;
(2)思路和辅助线同(1)证得Rt△OEB≌Rt△OFC后,可得出∠OBE=∠OCF,等腰△ABC中,∠ABC=∠ACB,因此∠OBC=∠OCB,那么OB=OC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC.
(1)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如示例图)


科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,那么抽中20元奖品的概率为
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
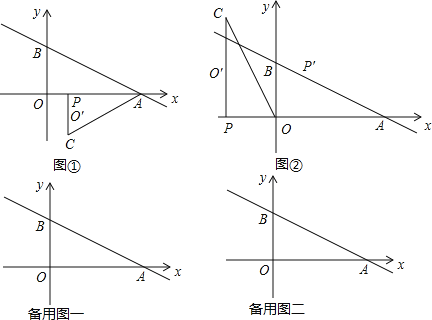
【题目】如图①,已知直线y=﹣![]() x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
(1)直接写出OA和OB的长,OA的长是 ,OB的长是 ;
(2)当点P在线段OA上(不含端点)时,求S关于m的函数表达式;
(3)当以A,P,C为顶点的三角形和△AOB相似时,求出所有满足条件的m的值;
(4)如图②,当点P关于OC的对称点P′落在直线AB上时,m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
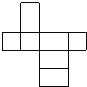
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形
D.四边相等的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),与y交于点C,∠BAC的平分线与y轴交于点D,与抛物线相交于点Q,P是线段AB上一点,过点P作x轴的垂线,分别交AD,AC于点E,F,连接BE,BF.
与x轴交于A,B两点(点A在点B的左侧),与y交于点C,∠BAC的平分线与y轴交于点D,与抛物线相交于点Q,P是线段AB上一点,过点P作x轴的垂线,分别交AD,AC于点E,F,连接BE,BF.
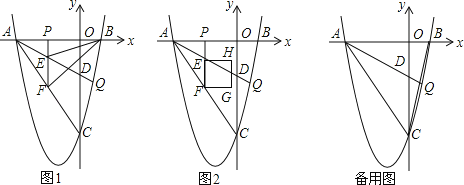
(1)如图1,求线段AC所在直线的解析式;
(2)如图1,求△BEF面积的最大值和此时点P的坐标;
(3)如图2,以EF为边,在它的右侧作正方形EFGH,点P在线段AB上运动时正方形EFGH也随之运动和变化,当正方形EFGH的顶点G或顶点H在线段BC上时,求正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.

(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com