
【题目】已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
【答案】(1). a=-1 ![]() (2). P1(
(2). P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
【解析】试题分析:(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-![]()
![]() +
+![]() ,其顶点坐标是
,其顶点坐标是![]() .
.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=![]() ,t2=-
,t2=-![]() .
.
∴此抛物线上的不动点有两个,即点P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:
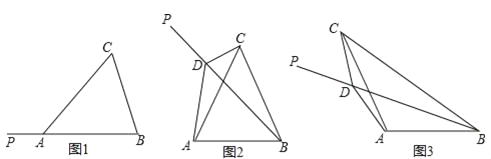
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:

(1)求∠CAD的度数;
(2)设AD、BC相交于E,AB、CD的延长线相交于F,求∠AEC、∠AFC的度数;
(3)若AD=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
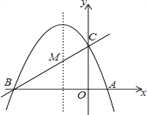
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别是三根木棒的长度,用它们能摆成三角形的是( )
A.4cm,4cm,9cmB.3cm,5cm,8cm
C.3cm,4cm,5cmD.1cm,2cm,3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的周长为1,连接△ABC的三边中点构成第二个三角形,再连接第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:_______________________;
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =________,
=________, ![]() =__________;
=__________;
②已知![]() =0.076 97,则
=0.076 97,则![]() =__________.
=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com