
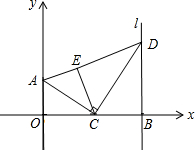
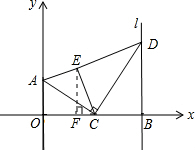
 ��ͼ����A�������ǣ�0��2������B��x���������ϵĵ㣬����B��ֱ��l��ֱ��x�ᣬ��CΪ�߶�OB�ϵĶ��㣬����AC������C��CD��AC��ֱ��l�ڵ�D������BCD��CD��������ECD��λ�ã�����AE�����B�������ǣ�m��0������C�������ǣ�n��0��
��ͼ����A�������ǣ�0��2������B��x���������ϵĵ㣬����B��ֱ��l��ֱ��x�ᣬ��CΪ�߶�OB�ϵĶ��㣬����AC������C��CD��AC��ֱ��l�ڵ�D������BCD��CD��������ECD��λ�ã�����AE�����B�������ǣ�m��0������C�������ǣ�n��0��| CB |
| AO |
| DB |
| OC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| CB |
| AO |
| DB |
| OC |
| m-n |
| 2 |
| DB |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 3 |
| 3 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��12�� | ||
B����4
| ||
C����8
| ||
| D��8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
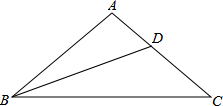 ���⣺�ڡ�ABC�У�AB=AC����A=100�㣬BDΪ��B��ƽ���ߣ�̽��AD��BD��BC֮���������ϵ��
���⣺�ڡ�ABC�У�AB=AC����A=100�㣬BDΪ��B��ƽ���ߣ�̽��AD��BD��BC֮���������ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
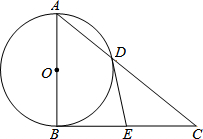 ��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC�ߵ��е㣬����DE��
��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC�ߵ��е㣬����DE��
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪AC��BC��BD��AD��AC��BD����O��AC=BD����֤��
��ͼ����֪AC��BC��BD��AD��AC��BD����O��AC=BD����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
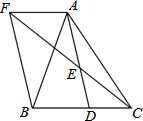 ��ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BF��ƽ���ߣ���CE���ӳ����ڵ�F����AF=BD������BF�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�
��ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BF��ƽ���ߣ���CE���ӳ����ڵ�F����AF=BD������BF�����AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
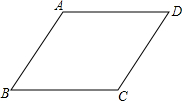 ��ͼ��������ABCD�У�AB=a����ABC=����������ABCD�Ƶ�B˳ʱ����ת����ת��С��90�㣩����A��C��D�ֱ�����A�䡢C�䡢D�䴦����A��C���BCʱA��D=
��ͼ��������ABCD�У�AB=a����ABC=����������ABCD�Ƶ�B˳ʱ����ת����ת��С��90�㣩����A��C��D�ֱ�����A�䡢C�䡢D�䴦����A��C���BCʱA��D=�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com