
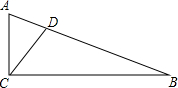
 如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$.
如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$. 分析 过D作DE⊥AC于E,DF⊥B于F,由于CD为△ABC的角平分线,于是得到DE=DF,由CD=2$\sqrt{2}$,得到DE=DF=2,根据三角形的面积得到$\frac{1}{2}$AC•DE$+\frac{1}{2}$BC•DF=AC+BC=10,$\frac{1}{2}$AC•BC=10,于是求得AC2+BC2=60,即可求得结果.
解答  解:过D作DE⊥AC于E,DF⊥B于F,
解:过D作DE⊥AC于E,DF⊥B于F,
∵CD为△ABC的角平分线,
∴DE=DF,
∵∠ACB=90°,
∴∠ACD=∠DCF=45°,
∵CD=2$\sqrt{2}$,∴DE=DF=2,
∵△ABC的面积为10,
∴$\frac{1}{2}$AC•DE$+\frac{1}{2}$BC•DF=AC+BC=10,$\frac{1}{2}$AC•BC=10,
∴(AC+BC)2=AC2+BC2+2AC•BC=100,
∴AC2+BC2=60,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{15}$.
故答案为:2$\sqrt{15}$.
点评 本题考查了角平分线的性质,三角形面积,正确的周长辅助线是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:解答题
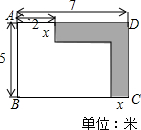 如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.
如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
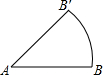 如图,将长度为2的线段AB绕点A逆时针旋转45°至AB′,则扇形ABB′的面积为( )
如图,将长度为2的线段AB绕点A逆时针旋转45°至AB′,则扇形ABB′的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $±\frac{1}{81}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
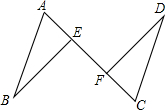 如图,线段AB∥CD,AB=CD=$\sqrt{10}$,连接AC,E、F是AC上的两点,且BE∥DF.
如图,线段AB∥CD,AB=CD=$\sqrt{10}$,连接AC,E、F是AC上的两点,且BE∥DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com