
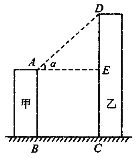
【题目】如图所示.线段AB、DC分别表示甲、乙两座建筑物的高.AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在A点测得D点的仰角α=45°,则乙建筑物高DC=______米.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
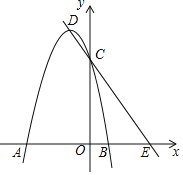
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,求抛物线顶点D的坐标,OE等于多少;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;
(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
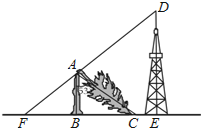
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
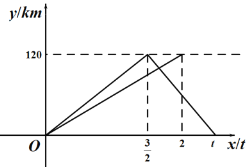
【题目】一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
(1)轿车从乙地返回甲地的速度为 km/t,t= h;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式;
(3)当轿车从甲地返回乙地的途中与货车相遇时,求相遇处到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 与反比例函数的图象交于点
与反比例函数的图象交于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
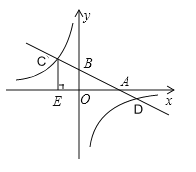
(1)求反比例函数及一次函数的解析式.
(2)当![]() 为何值时一次函数的值大于反比例函数的值.
为何值时一次函数的值大于反比例函数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com