
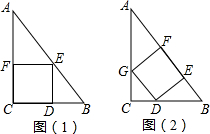
 ��֪��Rt��ABC�У���C=90�㣬BC=a��AC=b��AB=c�����������ڲü������Σ�ʹ�������ĸ�����ǡ���������εı��ϣ��������ֲ÷���
��֪��Rt��ABC�У���C=90�㣬BC=a��AC=b��AB=c�����������ڲü������Σ�ʹ�������ĸ�����ǡ���������εı��ϣ��������ֲ÷������� ��1���÷�1�������εı߳�Ϊx����EF��BC�����ǵõ���AEF�ס�ABC������$\frac{EF}{BC}$=$\frac{AF}{AC}$���ɵõ�x=$\frac{24}{7}$��
��2�����ݹ��ɶ����õ�c=10����б���ϵĸ�Ϊh�����������ε������ʽ��ab=ch�����h=4.8�õ�����ʽ$\frac{y}{10}=\frac{4.8-y}{4.8}$�����ɵõ�y=$\frac{120}{37}$��
��3���ɣ�1��֪��$\frac{x}{a}=\frac{b-x}{b}$���õ�x=$\frac{ab}{a+b}$���ɣ�2��֪$\frac{y}{c}=\frac{\frac{ab}{c}-y}{\frac{ab}{c}}$���õ�y=$\frac{ab}{c+\frac{ab}{c}}$�����ǵõ�$\frac{1}{y}$-$\frac{1}{x}$=$\frac{{c}^{2}+ab-��a+b��c}{abc}=\frac{��c-a����c-b��}{abc}$������c��a��c��b�����ǵõ���c-a����c-b����0�����$\frac{1}{y}-\frac{1}{x}$��0���õ�x��y�����ɵõ����ۣ�
��� �⣺��1���÷�1�������εı߳�Ϊx��
��EF��BC��
���AEF�ס�ABC��
��$\frac{EF}{BC}$=$\frac{AF}{AC}$��
��$\frac{x}{6}=\frac{8-x}{8}$��
��x=$\frac{24}{7}$��
��2����a=6��b=8��
��c=10��
��б���ϵĸ�Ϊh�����������ε������ʽ��ab=ch��
��h=4.8��
�߲÷�2�������εı߳�y����$\frac{y}{10}=\frac{4.8-y}{4.8}$��
��ã�y=$\frac{120}{37}$��
��3��S1��S2�����ɣ�
�ɣ�1��֪��$\frac{x}{a}=\frac{b-x}{b}$����bx=ab-ax��
��x=$\frac{ab}{a+b}$��
�ɣ�2��֪$\frac{y}{c}=\frac{\frac{ab}{c}-y}{\frac{ab}{c}}$����y=$\frac{abc}{{c}^{2}+ab}$��
��y=$\frac{ab}{c+\frac{ab}{c}}$��
��$\frac{1}{y}$-$\frac{1}{x}$=$\frac{c+\frac{ab}{c}}{ab}-\frac{a+b}{ab}$=$\frac{c+\frac{ab}{c}-��a+b��}{ab}$=$\frac{{c}^{2}+ab-��a+b��c}{abc}=\frac{��c-a����c-b��}{abc}$��
��c��a��c��b��
�ࣨc-a����c-b����0��
��$\frac{1}{y}-\frac{1}{x}$��0��
��$\frac{1}{y}��\frac{1}{x}$��
��x��y�����÷�1�õ��������α߳����÷�2�õ��������α߳���
��S1��S2��
���� ���⿼�������������ε��ж������ʣ������ε����ʣ������ε������ʽ�����ɶ������������ո����ʶ����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | -5 | C�� | -4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
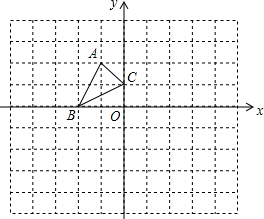 ��ABCƽ����ֱ������ϵ�е�λ����ͼ��ʾ������ÿ��С�����εı߳���Ϊ1������A��-1��2������B��-2��0������C��0��1����
��ABCƽ����ֱ������ϵ�е�λ����ͼ��ʾ������ÿ��С�����εı߳���Ϊ1������A��-1��2������B��-2��0������C��0��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
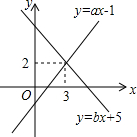 һ�κ���y=ax-1��y=bx+5��ͼ����ͼ��ʾ����a��b��ֵ�ǣ�������
һ�κ���y=ax-1��y=bx+5��ͼ����ͼ��ʾ����a��b��ֵ�ǣ�������| A�� | a=3��b=2 | B�� | a=2��b=3 | C�� | a=1��b=-1 | D�� | a=-1��b=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
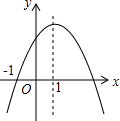 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����������н��ۣ�
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 17cm | B�� | 16cm | C�� | 4cm | D�� | 5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ǺͶ۽�һ������ | B�� | һ���ǵIJ���һ����������� | ||
| C�� | �������ȷ��������ֱ�� | D�� | �۽ǵIJ���һ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8% | B�� | 18% | C�� | 20% | D�� | 25% |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com