
����Ŀ��ij�з��躽ģС�ӣ��ƻ�����һ�����˻�����֪3̨A�����˻���4̨B�����˻�����6400Ԫ��4̨A�����˻���3̨B�����˻�����6200Ԫ��
��1����һ̨A�����˻���һ̨B�����˻����ۼ۸��Ƕ���Ԫ��
��2���ú�ģС��һ�ι��������ͺŵ����˻���50̨������B�����˻�������������A�����˻���������2�����蹺��A�����˻�x̨���ܷ���ΪyԪ��
����y��x�Ĺ�ϵʽ��
�ڹ���A�͡�B�����˻�������̨������ʹ�ܷ������٣�
���𰸡���1��һ̨A�����˻��ۼ�800Ԫ��һ̨B�����˻����ۼ�1000Ԫ��
��2����y����200x+50000���ڹ���A�͡�B�����˻���16̨��34̨ʱ������ʹ�ܷ������٣�
��������
��1������3̨A�����˻���4̨B�����˻�����6400Ԫ��4̨A�����˻���3̨B�����˻�����6200Ԫ�������г���Ӧ�ķ����飬�Ӷ����Խ���⣻
��2���ٸ���������Եõ�y��x�ĺ�����ϵʽ��
�ڸ��ݢ��еĺ�����ϵʽ��B�����˻�������������A�����˻���������2����������ù���A�͡�B�����˻�������̨������ʹ�ܷ������٣�
�⣺��1����һ̨![]() �����˻��ۼ�
�����˻��ۼ�![]() Ԫ��һ̨
Ԫ��һ̨![]() �����˻����ۼ�
�����˻����ۼ�![]() Ԫ��
Ԫ��
![]() ��
��
��ã�![]() ��
��
��һ̨![]() �����˻��ۼ�
�����˻��ۼ�![]() Ԫ��һ̨
Ԫ��һ̨![]() �����˻����ۼ�
�����˻����ۼ�![]() Ԫ��
Ԫ��
��2����������ɵã�
![]()
��y��x�ĺ�����ϵʽΪ![]() ��
��
�ڡ�B�����˻�������������A�����˻���������2����
![]() ��
��
��ã�![]() ��
��
![]() ��
��
�൱![]() ʱ��yȡ����Сֵ����ʱ
ʱ��yȡ����Сֵ����ʱ![]() ��
��
�𣺹���![]() �͡�
�͡�![]() �����˻���
�����˻���![]() ̨��
̨��![]() ̨ʱ������ʹ�ܷ������٣�
̨ʱ������ʹ�ܷ������٣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
ij�̳���8��Ԫ����һ���¿�������ϼܺ�ܿ�����һ�գ��̳��ֽ��������ڶ������ֳ����������ǵ�һ�ε�2��������������4Ԫ/�����������ȥ17.6��Ԫ��
��1�����̳���һ�������������ټ���
��2���̳��������ֳ���ʱ��ÿ�����۶���58Ԫ��ʣ��150��ʱ�����۳��ۣ�ȫ�����꣮�����������������̳���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x��1����x���һ����������Ϊ����1��0���䲿��ͼ����ͼ��ʾ�����н��ۣ���b2��4ac��0���ڷ���ax2+bx+c����������x1����1��x2��3�� ��2a+b��0���ܵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3���ݵ�x��0��y��x�������С�����н�����ȷ�������_____��
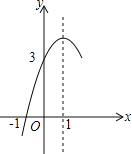
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����λͬѧ���о�����y��ax2+bx+c(a��b��cΪ��������a��0)ʱ�����ֵ�x��1ʱ�����������ֵ���ҷ��֩�1�Ƿ���ax2+bx+c��0��һ�����������ֺ��������ֵΪ��1�������ֵ�x��2ʱ��y����2����֪��λ��ֻ��һλ���ֵĽ���ʱ����ģ����ͬѧ��( ).
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P����Ϊ��1��![]() ������OPΪб��������ֱ�ǡ�OAP��ֱ�Ƕ���A�ڷ���������y��
������OPΪб��������ֱ�ǡ�OAP��ֱ�Ƕ���A�ڷ���������y��![]() ��ͼ���ϣ���k��ֵ��_____��
��ͼ���ϣ���k��ֵ��_____��
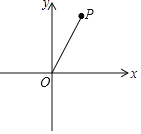
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����ֱ�Ķ�������l����һ��Ϊ1.5km����ͷMN�͵���C������C����ͷ�Ķ���N��20km.һ�ִ���36km/h���ٶȺ��У�����10��00��A����õ���Cλ���ִ��ı�ƫ��30����������10��40��B����õ���Cλ���ִ��ı�ƫ��60�������������C���12km.
(1)���ִ��մ��ٶ��뺽����ʱ���ﺣ���ߣ�
(2)���ִ����ı亽���ִ��ܷ�ͣ������ͷ����˵������(�ο����ݣ� ![]() ��1.4��
��1.4�� ![]() ��1.7)��
��1.7)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABCD�У�AE��BC��E��EǡΪBC���е㣮tanB��2��
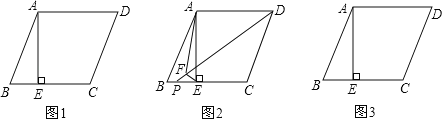
��1����֤��AD��AE��
��2����ͼ2����P��BE�ϣ���EF��DP�ڵ�F������AF���߶�DF��EF��AF֮����������������ϵ����˵�����ɣ�
��3��������ͼ3�л�ͼ̽������PΪ����EC��������һ�㣨P�����E�غϣ�ʱ����EF��DP�ڵ�F������AF���߶�DF��EF��AF֮����������������ϵ������ͼ3�в�ȫͼ�Σ�ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3cm������M�ӵ�B������3cm/s���ٶ����ű�BC��CD��DA�˶��������Aֹͣ�˶�����һ����Nͬʱ�ӵ�B��������1cm/s���ٶ����ű�BA���A�˶��������Aֹͣ�˶������M�˶�ʱ��Ϊx��s������AMN�����Ϊy��cm2������y����x�ĺ���ͼ���ǣ�������

A.  B.
B. 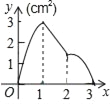 C.
C.  D.
D. 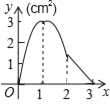
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABCD����E��BC���ϵ�һ��������AD�ӳ�����F��ʹ��AFC����DEC.

(1)��֤���ı���DECF��ƽ���ı��Σ�
(2)��AB��13��DF��14��tan A��![]() ����CF�ij���
����CF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com