
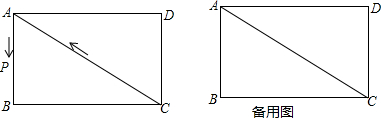
���� ��1��������ʽ�ֽⷨ������̼��ɣ�
��2�����ݹ��ɶ����г����̣��ⷽ�̼��ɣ�
��3����PC=CD��PD=PC��PD=CD������������ݵ��������ε����ʺ��ɶ������㼴�ɣ�
��� �⣺��1����x2-7x+12=0��
��x-3����x-4��=0��
��x1=3��x2=4��
��AB=3��BC=4��
��2���������${3^2}+{��t-3��^2}=\sqrt{10}$��
��t1=4��t2=2����ȥ����
��t=4ʱ��AP=$\sqrt{10}$��
��3�����ڵ�P��ʹ��CDP�ǵ��������Σ�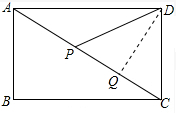
�ٵ�PC=CD=3ʱ��t=��3+4+3����1=10���룩��
�ڵ�PD=PC����PΪ�Խ���AC�е㣩ʱ��AB=3��BC=4��
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5��CP=$\frac{1}{2}$AC=2.5��
��t=��3+4+2.5����1=9.5���룩��
�۵�PD=CD=3ʱ����DQ��AC��Q��
$DQ=\frac{{\frac{1}{2}��3��4}}{{\frac{1}{2}��5}}=\frac{12}{5}$��$PQ=\sqrt{{3^2}-{{��\frac{12}{5}��}^2}}=\frac{9}{5}$��
��PC=2PQ=$\frac{18}{5}$��
��$t=\frac{{3+4+\frac{18}{5}}}{1}=\frac{53}{5}$���룩��
��֪��tΪ10���9.5���$\frac{53}{5}$��ʱ����CDP�ǵ��������Σ�
���� ���⿼����Ǿ��ε����ʡ����������ε��ж��������Լ�һԪ���η��̵Ľⷨ����ȷ������̡�������ù��ɶ����г���ʽ�ǽ���Ĺؼ���ע����������˼������ã�


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
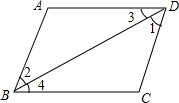 ��ͼ����֪��1=��2�����ڽ��ۣ���1����3=��4����2��AB��CD����3��AD��BC��������
��ͼ����֪��1=��2�����ڽ��ۣ���1����3=��4����2��AB��CD����3��AD��BC��������| A�� | ֻ��һ����ȷ | B�� | ֻ��һ������ȷ | C�� | ��������ȷ | D�� | ����������ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ÿ��С�����εı߳�Ϊ1����λ��ÿ��С����Ķ���и�㣮
��ͼ��ÿ��С�����εı߳�Ϊ1����λ��ÿ��С����Ķ���и�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
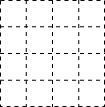 �����������е�ÿ��С�����α߳���1��ÿ��С��Ķ��������㣬�Ը��Ϊ���㰴����Ҫ�������Σ�
�����������е�ÿ��С�����α߳���1��ÿ��С��Ķ��������㣬�Ը��Ϊ���㰴����Ҫ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com