
【题目】如图,![]() 是等腰直角
是等腰直角![]() 外一点,把
外一点,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() .已知
.已知![]() .则
.则![]() ________.
________.
【答案】![]()
【解析】
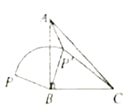
连接AP,根据同角的余角相等可得∠ABP=∠CBP′,然后利用“边角边”证明△ABP和△CBP′全等,根据全等三角形对应边相等可得AP=CP′,连接PP′,根据旋转的性质可得△PBP′是等腰直角三角形,然后求出∠AP′P是直角,再利用勾股定理用AP′表示出PP′,又等腰直角三角形的斜边等于直角边的![]() 倍,代入整理即可得解.
倍,代入整理即可得解.
如图,连接AP,∵BP绕点B顺时针旋转90°到BP′,

∴BP=BP′,∠ABP+∠ABP′=90°,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=90°,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
∵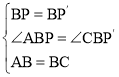 ,
,
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
连接PP′,则△PBP′是等腰直角三角形,
∴∠BP′P=45°,PP′=![]() PB,
PB,
∵∠AP′B=135°,
∴∠AP′P=135°﹣45°=90°,
∴△APP′是直角三角形,
设P′A=x,则AP=3x,
根据勾股定理,PP′=![]() ,
,
∴PP′=![]() PB=2
PB=2![]() x,
x,
解得PB=2x,
∴P′A:PB=x:2x=1:2.
故答案是:1:2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-3,-3),B(-1,-3)C(-1, 0).

(1)画出△ABC
(2)画出△ABC关于x轴对称的![]() ,并写出点
,并写出点![]() 的坐标:
的坐标:
(3)以点O为位似中心,在第一象限内把△ABC放大到原来的两倍后得到![]() ,写出点
,写出点![]() 的坐标:
的坐标:
查看答案和解析>>
科目:初中数学 来源: 题型:
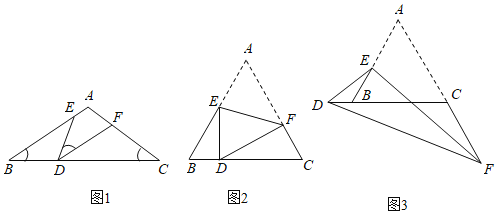
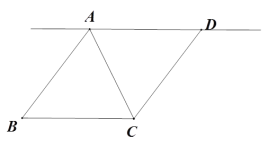
【题目】(1)模型探究:如图1,D、E、F分别为△ABC三边BC、AB、AC上的点,且∠B=∠C=∠EDF=a.△BDE与△CFD相似吗?请说明理由;
(2)模型应用:△ABC为等边三角形,其边长为8,E为AB边上一点,F为射线AC上一点,将△AEF沿EF翻折,使A点落在射线CB上的点D处,且BD=2.
①如图2,当点D在线段BC上时,求![]() 的值;
的值;
②如图3,当点D落在线段CB的延长线上时,求△BDE与△CFD的周长之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.

(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() 、顶点
、顶点![]() 的横坐标为.
的横坐标为.
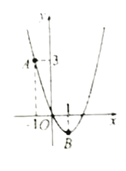
(1)求这个二次函数的解析式;
(2)点![]() 在该一次函数的图象上,点
在该一次函数的图象上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点D是△ABC中BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是点EF,且BF=CE.
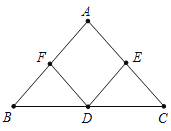
(1)求证:Rt△BDF≌Rt△CDE
(2)问:△ABC满足什么条件时,四边形AEDF是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com