练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若4x=$\frac{1}{2•\root{3}{2}}$，那么x=-$\frac{3}{4}$．

    分析 两边长以2•$\root{3}{2}$，再把底数都化为2，接着根据同底数幂的乘法计算，然后根据零指数幂的意义得到关于x的方程，再解方程即可．

    解答 解：∵4x=$\frac{1}{2•\root{3}{2}}$，
    ∴22x•2•${2}^{\frac{1}{3}}$=1，
    即${2}^{2x+1+\frac{1}{3}}$=1，
    ∴2x+1+$\frac{1}{2}$=0，
    ∴x=-$\frac{3}{4}$．
    故答案为-$\frac{3}{4}$．

    点评 本题考查了分数指数：${a}^{\frac{q}{p}}$=$\root{p}{{a}^{q}}$（p、q为正整数，a≠0）．也考查了幂的运算和零指数幂的意义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，∠BAC=90°，∠EDC=90°，∠DCE=30°，ED=2，AB=3，求S△CEB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在?ABCD中．点O是对角线AC、BD的交点，AC垂直于BC．且AB=10cm，AD=8cm，求OB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知点P（x，y）在第三象限，则化简$\sqrt{（{x}^{2}+{y}^{2}）^{2}-（{x}^{2}-{{y}^{2}）}^{2}}$的结果是（　　）
    A．2xyB．-2xyC．2D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．在实数范围内，因式分解：x4-11x2+28=（x+2）（x+$\sqrt{2}$）（x-$\sqrt{2}$）（x+$\sqrt{7}$）（x-$\sqrt{7}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知a＜-6，|3-$\sqrt{{a}^{2}+6a+9}$|=-a-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化筒，再求代数式$\frac{4{y}^{2}-{x}^{2}}{-{x}^{2}-4{y}^{2}+4xy}$的值，其中x=$\frac{5}{4}$，y=$-\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+（m-1）y=4}\\{nx+y=2}\end{array}\right.$的解，求（m+n）2014的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

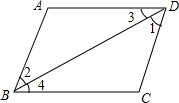    18．如图，已知∠1=∠2，则在结论：（1）∠3=∠4，（2）AB∥CD，（3）AD∥BC（　　）
    A．只有一个正确B．只有一个不正确C．三个都正确D．三个都不正确

    查看答案和解析>>

    同步练习册答案