
【题目】如图,AB为半圆O的直径,点C为半圆上任一点.
(1)若∠BAC=30°,过点C作半圆O的切线交直线AB于点P.求证:△PBC≌△AOC;
(2)若AB=6,过点C作AB的平行线交半圆O于点D.当以点A,O,C,D为顶点的四边形为菱形时,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)π或2π.
【解析】
(1)根据圆周角定理得到∠ACB=90°,推出△OBC是等边三角形,根据等边三角形和外角的性质得到∠AOC=∠PBC=120°,根据切线的性质得到∠OCP=90°,根据全等三角形的判定即可得到结论;
(2)根据菱形的性质得到OA=AD=CD=OC,连接OD,得到△AOD与△COD是等边三角形,根据等边三角形的性质得到∠AOD=∠COD=60°,求得∠BOC=60°,同理可得另一种情况∠BOC=120°,然后根据弧长公式即可得到结论,.
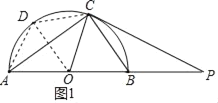
解:(1)如图1,∵AB为半圆O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴∠ABC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OC=BC,∠OBC=∠BOC=60°,
∴∠AOC=∠PBC=120°,
∵CP是⊙O的切线,
∴OC⊥PC,
∴∠OCP=90°,
∴∠ACO=∠PCB,
在△PBC与△AOC中,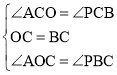 ,
,
∴△PBC≌△AOC(ASA);
(2)如图1,连接OD,BD,CD,
∵四边形AOCD是菱形,
∴OA=AD=CD=OC,
∵OA=OD=OC,
∴△AOD与△COD是等边三角形,
∴∠AOD=∠COD=60°,
∴∠BOC=60°,
∴![]() 的长=
的长=![]() =π;
=π;
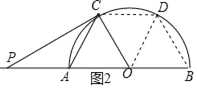
如图2,同理∠BOC=120°,
∴![]() 的长=
的长=![]() =2π,
=2π,
综上所述,![]() 的长为π或2π.
的长为π或2π.


科目:初中数学 来源: 题型:
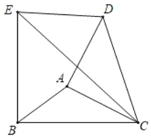
【题目】如图,分别以△ABC中BC和AC为腰向外作等腰直角△EBC和等腰直角△DAC,连结DE,且DE∥BC,EB=BC=6,四边形EBCD的面积为24,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
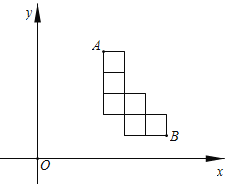
查看答案和解析>>
科目:初中数学 来源: 题型:
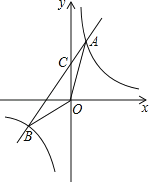
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
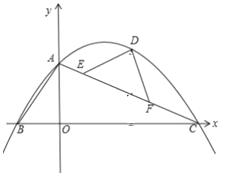
【题目】如图,平面直角坐标系中,O为坐标原点,直线y=﹣![]() x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=
x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=![]() .
.
(1)求抛物线的解析式;
(2)已知E、F是线段AC上异于A、C的两个点,且AE<AF,EF=2![]() ,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
(3)在(2)的条件下,当∠EDF=90°时,连接BD,P为抛物线上一动点,过P作PQ⊥BD交线段BD于点Q,连接EQ.设点P的横坐标为t,求t为何值时,PE=QE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,定义:直线![]() 与x、y轴分别相交于A、B两点,将
与x、y轴分别相交于A、B两点,将![]() 绕着点O逆时针旋转90°得到
绕着点O逆时针旋转90°得到![]() ,过点A、B、D的抛物线P叫做直线
,过点A、B、D的抛物线P叫做直线![]() 的“纠缠抛物线”,反之,直线
的“纠缠抛物线”,反之,直线![]() 叫做P的“纠缠直线",两线“互为纠缠线”.
叫做P的“纠缠直线",两线“互为纠缠线”.
(1)若![]() ,则纠缠物线P的函数解析式是____________.
,则纠缠物线P的函数解析式是____________.
(2)判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
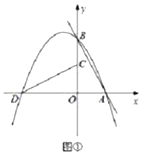
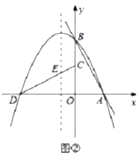
(3)如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与
,纠缠抛物线P的对称轴与![]() 相交于点E,点F在
相交于点E,点F在![]() 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以
上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以![]() 为一边的平行四边形时,求点Q的坐标.
为一边的平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com