【题目】如图，矩形ABCD中，AB＝3，BC＝5．过对角线交点O作OE⊥AC交AD于E，则AE的长是（ ）
A.1.6
B.2.5
C.3
D.3.4
【答案】D
【解析】连接EC，由矩形的性质可得AO＝CO，
又因EO⊥AC，
则由线段的垂直平分线的性质可得EC＝AE，
设AE＝x，则ED＝AD﹣AE＝5﹣x，
在Rt△EDC中，根据勾股定理可得EC2＝DE2+DC2 ，
即x2＝（5﹣x）2+32 ，
解得x＝3.4．
故选D．
【考点精析】本题主要考查了线段垂直平分线的性质和勾股定理的概念的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．
科目：初中数学 来源： 题型：
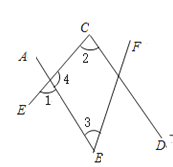
【题目】如图，∠1和∠2是直线_______和直线________被直线______所截得的同位角；
∠1和∠3是直线_______和直线________被直线______所截得的__________角；
∠2和∠4是直线_______和直线________被直线______所截得的__________角；
∠3和∠4是直线_______和直线________被直线______所截得的__________角；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．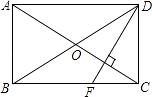 
（1）求证：四边形ABCD是矩形．
（2）若∠ADF：∠FDC=3：2，DF⊥AC，则∠BDF的度数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB＝1，AD＝2，M是CD的中点，点P在矩形的边上沿ABCM运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的（ ）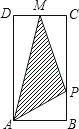
A.
B.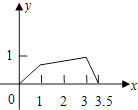
C.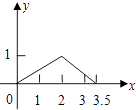 
D.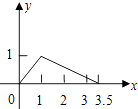
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列关于x的单项式，探究其规律： x，3x2 ， 5x3 ， 7x4 ， 9x5 ， 11x6 ， …
按照上述规律，第2015个单项式是（ ）
A.2015x2015
B.4029x2014
C.4029x2015
D.4031x2015
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）若a、b互为相反数，b、c互为负倒数，并且m的立方等于它本身．
（1）试求
﹣ac值；
（2）若a＞1，且m=﹣1，S=|2a﹣3b|﹣2|b﹣m|﹣|b+
|，试求4（2a﹣S）+2（2a﹣S）﹣（2a﹣S）的值．
（3）若m＞0，且x为有理数时，|x+m|﹣|x﹣m|+1是否存在最大值，若存在，求出这个最大值，并求出x的取值范围；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司销售一种进价为20元/个的计算器，其销售量y（万个）与销售价格x（元/个）的变化如下表：
价格x（元/个） | … | 30 | 40 | 50 | 60 | … |
销售量y（万个） | … | 5 | 4 | 3 | 2 | … |
同时，销售过程中的其他开支（不含进价）总计40万元．
（1）观察并分析表中的y与x之间的对应关系，用所学过的一次函数，反比例函数或二次函数的有关知识写出y（万个）与x（元/个）的函数解析式．
（2）求出该公司销售这种计算器的净得利润z（万元）与销售价格x（元/个）的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？
（3）该公司要求净得利润不能低于40万元，请写出销售价格x（元/个）的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（ ）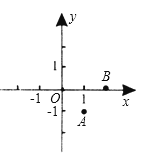
A.（3，-1）
B.（-1，-1）
C.（1，1）
D.（-2，-1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com