
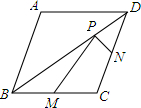
 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).
已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).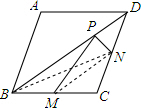
| 1 |
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )
如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )| A、120° | B、150° |
| C、75° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、某射击运动员射击一次,命中靶心 |
| B、经过城市中某一有交通信号的路口,遇到红灯 |
| C、抛掷一枚硬币,正面向上 |
| D、掷一枚骰子,点数大于0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com