
 如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=
如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=| 1 |
| 4 |
| BA |
| a |
| BC |
| b |
| a |
| b |
| FD |
| FC |
| BA |
| a |
| BC |
| b |
| CD |
| AC |
| CD |
| BA |
| a |
| AC |
| BC |
| BA |
| b |
| a |
| EC |
| 1 |
| 4 |
| BC |
| 1 |
| 4 |
| b |
| ED |
| EC |
| CD |
| 1 |
| 4 |
| b |
| a |
| DF |
| FE |
| AF |
| FC |
| AD |
| EC |
| 1 |
| 4 |
| DF |
| FE |
| AF |
| FC |
| 1 |
| 4 |
| FD |
| 4 |
| 5 |
| ED |
| 4 |
| 5 |
| 1 |
| 4 |
| b |
| a |
| 1 |
| 5 |
| b |
| 4 |
| 5 |
| a |
| FC |
| 1 |
| 5 |
| AC |
| 1 |
| 5 |
| b |
| 1 |
| 5 |
| a |


科目:初中数学 来源: 题型:
 如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°,试求∠DEG与∠BGD′的度数.
如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°,试求∠DEG与∠BGD′的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
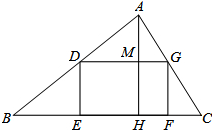 如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长.
如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,等边三角形ABC中,点D,E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE,AD,EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.
已知,如图,等边三角形ABC中,点D,E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE,AD,EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com