
【题目】阅读材料:
在平面直角坐标系![]() 中,点
中,点![]() 到直线
到直线![]() 的距离公式为
的距离公式为![]() .
.
例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线![]() 知,
知,![]() ,
,![]() ,
,![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
根据以上材料,解决下列问题:
问题1:点![]() 到直线
到直线![]() 的距离为__________;
的距离为__________;
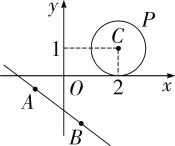
问题2:已知![]() 是以点
是以点![]() 为圆心,1为半径的圆,
为圆心,1为半径的圆,![]() 与直线
与直线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
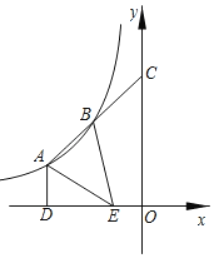
问题3:如图,设点![]() 为问题2中
为问题2中![]() 上的任意一点,点
上的任意一点,点![]() 、
、![]() 为直线
为直线![]() 上的两点,且
上的两点,且![]() 请求出
请求出![]() 的最大值和最小值.
的最大值和最小值.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
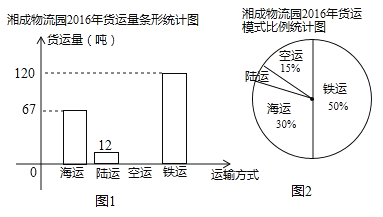
【题目】在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
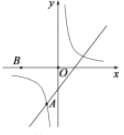
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 在第三象限交于点
在第三象限交于点![]() .点
.点![]() 的坐标为(一3,0),点
的坐标为(一3,0),点![]() 是
是![]() 轴左侧的一点.若以
轴左侧的一点.若以![]() 为顶点的四边形为平行四边形.则点
为顶点的四边形为平行四边形.则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
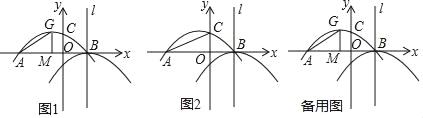
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
A.﹣12B.﹣10C.﹣9D.﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020春节期间,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩防护用品销售量暴涨、供应紧张,国有疫,我有责,在特殊时期,某集团紧急启动了应急响应机制,取消了工人休假,与疫情救灾相关的口罩、防护服生产线连续24小时运转,将援驰武汉的120万片口罩和8万防护服第一时间发往武汉,其中120万用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com