
 如图是小明设计的用激光笔测量城墙高度的示意图,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么该城墙高度CD=8米.
如图是小明设计的用激光笔测量城墙高度的示意图,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么该城墙高度CD=8米.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )
如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )| A. | (1,-2) | B. | (-2,1) | C. | (-2,2) | D. | (2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
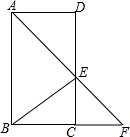 如图,在?ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
如图,在?ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k<1 | C. | k>0 | D. | k<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
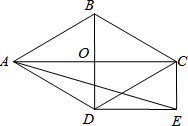 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
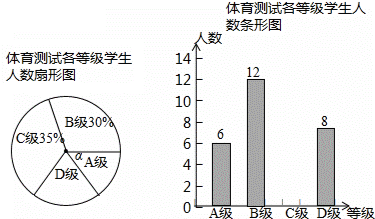
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com