
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
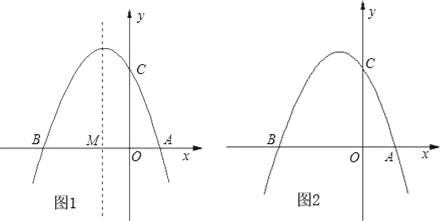
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
【答案】解:(1)![]()
(2)存在P1(-1, ![]() )、P2(1,6),P3(1,
)、P2(1,6),P3(1, ![]() )
)
(3)连OE设四边形BOCE的面积为S,点E的坐标为(![]() )
)
∵E在第二象限
∴3<x<0 -x2-2x+3>0
∵S=S△BOE+S△COE=![]() +
+![]() ×3×(-×)
×3×(-×)
=![]()
∵-3<x<0
∴当x=-![]() 时,S最大为
时,S最大为![]()
此时,E(![]() )
)
【解析】试题分析:(1)利用待定系数法求函数解析式即可;(2)分CP=MP、CM=CP、CM=MP三种情况讨论,(3)过点E作EF⊥x轴于点F,设E(a,-![]() -2a+3)(-3<a<0),然后用a表示出四边形BOCE面积,然后利用二次函数的性质确定最大值即可得到点E坐标.
-2a+3)(-3<a<0),然后用a表示出四边形BOCE面积,然后利用二次函数的性质确定最大值即可得到点E坐标.
试题解析:解︰(1)由题知︰![]() ,解得︰
,解得︰![]()
∴所求抛物线解析式为︰![]()
(2)存在符合条件的点P,
其坐标为P(-1,![]() )或P(-1,-
)或P(-1,-![]() )或P(-1,6)或P(-1,
)或P(-1,6)或P(-1,![]() )
)
(3)解法①:
过点E作EF⊥x轴于点F,设E(a,-![]() -2a+3)(-3<a<0)
-2a+3)(-3<a<0)
∴EF=-![]() -2a+3,BF=a+3,OF=-a
-2a+3,BF=a+3,OF=-a
∴S四边形BOCE=![]() BF·EF+
BF·EF+![]() (OC+EF)·OF
(OC+EF)·OF
=![]() (a+3)·(-
(a+3)·(-![]() -2a+3)+
-2a+3)+![]() (-
(-![]() -2a+6)·(-a)
-2a+6)·(-a)
=![]() =-
=-![]()
![]() +
+![]()
∴当a=-![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() .
.
此时,点E坐标为(-![]() ,
,![]() )
)
解法②:
过点E作EF⊥x轴于点F,设E(x,y)(-3<x<0)
则S四边形BOCE=![]() (3+y)·(-x)+
(3+y)·(-x)+![]() (3+x)·y
(3+x)·y
=![]() (y-x)=
(y-x)=![]() (
(![]() )=-
)=-![]()
![]() +
+![]()
∴当x=-![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() .此时,点E坐标为(-
.此时,点E坐标为(-![]() ,
,![]() )
)


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
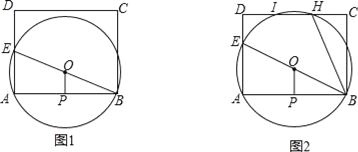
【题目】如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP,
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(5,6)与点B关于x轴对称,则点B的坐标为( )
A. (5,6) B. (-5,-6) C. (-5,6) D. (5,-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com