Question

3．已知A（2，m），B（n，-1）是双曲线y=-$\frac{6}{x}$上的两点，求△AOB的面积．

Answer 1

分析 将点A与B的坐标分别代入双曲线的解析式求出A、B两点的坐标，然后作图求△AOB的面积即可．

解答 解：∵A（2，m），B（n，-1）是双曲线y=-$\frac{6}{x}$上的两点，
∴2m=-6，-n=-6
∴m=-3，n=6
∴A（2，-3），B（6，-1）
如下图所示：作BN⊥x轴于点N，作AM⊥y轴于点M，BC⊥y轴于点C，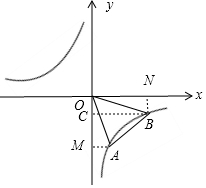

则：S_△AOB=S_矩形ONBC+S_梯形ABCM-S_△OAM-S_△OBN=6×1+$\frac{1}{2}$（2+6）×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×6×1=8
即：△AOB的面积为5

点评 本题考查了反比例函数系数k的几何意义，解题的关键是求出出A、B两点的坐标，将S_△AOB看作是S_矩形ONBC+S_梯形ABCM-S_△OAM-S_△OBN．