
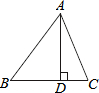
 如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.
如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看. 分析 由勾股定理求出BD、CD,得出BC,由三角形的面积公式即可得出结果.
解答 解:能求得△ABC的面积;理由如下:
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2-AD2=152-122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
∴BC=BD+DC=9+5=14,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×14×12=84.
点评 本题考查了勾股定理、三角形面积的计算方法;熟练掌握勾股定理,由勾股定理求出BC是解决问题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:选择题
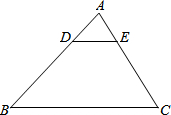 如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
如图,△ABC中,DE∥BC,则下列等式中不成立的是( )| A. | $\frac{AD}{DB}=\frac{AE}{EC}$ | B. | $\frac{AD}{AB}=\frac{AE}{AC}$ | C. | $\frac{AD}{AB}=\frac{DE}{BC}$ | D. | $\frac{AD}{AE}=\frac{DE}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
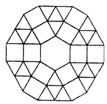 某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)
某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com