
分析 (1)归纳总结得到第九项,确定出第n项即可;
(2)方程利用拆项法变形,计算即可求出解.
解答 解:(1)第九项为$\frac{1}{9×10}$;第n项是$\frac{1}{n(n+1)}$;
(2)方程整理得:$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$+…+$\frac{1}{x+2001}$-$\frac{1}{x+2002}$=1-$\frac{1}{x+2002}$,
整理得:$\frac{1}{x+1}$-$\frac{1}{x+2002}$=1-$\frac{1}{x+2002}$,即$\frac{1}{x+1}$=1,
解得:x=0,
经检验x=0是分式方程的解.
故答案为:(1)$\frac{1}{9×10}$;$\frac{1}{n(n+1)}$
点评 此题考查了解分式方程,以及分式的加减法,熟练掌握运算法则是解本题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
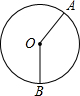 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )| A. | 40°和50° | B. | 80°和100° | C. | 120°和150° | D. | 160°和200° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com