练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1，已知中，，，点在边上，过点作的垂线与过点垂直的直线交于点．

    （1）求证：；

    （2）如图2，若点为线段的中点，连接交于，请直接写出图中所有的等腰直角三角形．

    【答案】（1）详见解析；（2）（2），，，

    【解析】

    （1）通过证明，可得CD=BE

    （2）由等腰直角三角形的判定可求解．

    （1）∵，

    ∴，

    ∴，且

    ∴，且AC=BC

    ，

    ∴(AAS)

    ∴CD=BE

    （2）

    ∵点为线段的中点

    ∴CD=BD=BE，且∠DBE=

    ∴△DBE是等腰直角三角形，
    ∴∠BDE=∠BED=

    ∵∠ACB=，AC=CB

    ∴△ABC是等腰直角三角形，∠ABC=

    ∴∠BDE=∠BED==∠ABC=∠EBF

    ∴DF=BF=EF，BF⊥DE
    ∴△DBF，△BFE是等腰直角三角形．

    故，，，是等腰直角三角形

    故答案为：，，，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在R△ABC中，∠ACB＝90°，AC＝6，BC＝8，E为AC上一点，且AE＝，AD平分∠BAC交BC于D．若P是AD上的动点，则PC+PE的最小值等于（　　）

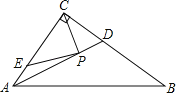
    A.B.C.4D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为

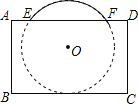
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学课上，老师提出如下问题：如何使用尺规完成“过直线l外一点P作已知直线l的平行线”．

    小明的作法如下：

    ①在直线l上取一点A，以点A为圆心，AP长为半径作弧，交直线l于点B；

    ②分别以P，B为圆心，以AP长为半径作弧，两弧相交于点Q（与点A不重合）；

    ③作直线PQ．所以直线PQ就是所求作的直线．根据小明的作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明．

    证明：∵AB＝AP＝　 　＝　 　．

    ∴四边形ABQP是菱形（　 　）（填推理的依据）．

    ∴PQ∥l．

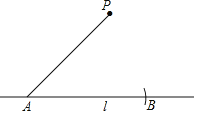
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形中，，点为边上一动点(与点不重合)，连接将的两边所在射线以点为中心，顺时针旋转分别交射线于点．

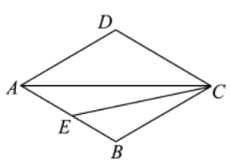
    （1）依题意补全图形；

    （2）若，求的大小(用含的式子表示) ；

    （3）用等式表示线段与之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于两点，是以点为圆心，为半径的圆上的动点，是线段的中点，连接，则线段的最小值是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠BAC=90°，点D是边BC上的动点，连接AD，点C关于直线AD的对称点为点E，射线BE与射线AD交于点F.

    （1）在图1中，依题意补全图形；

    （2）记（），求的大小；（用含的式子表示）

    （3）若△ACE是等边三角形，猜想EF和BC的数量关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    对于任意正实数a、b，

    ∵，

    当且仅当时，等号成立．

    结论：在均为正实数)中，若为定值则当且仅当时，a+b有最小值．

    拓展：对于任意正实数，都有当且仅当时，等号成立．

    在(a、b、c均为正实数)中，若为定值，则当且仅当时，有最小值

    例如：则，当且仅当，即时等号成立．

    又如：若求的最小值时，因为当且仅当，即时等号成立，故当时，有最小值．

    根据上述材料，解答下列问题：

    （1）若a为正数，则当a=______时，代数式取得最小值，最小值为_____；

    （2）已知函数与函数，求函数的最小值及此时的值；

    （3）我国某大型空载机的一次空载运输成本包含三部分：一是基本运输费用，共8100元；二是飞行耗油，每一百公里1200元；三是飞行报耗费用，飞行报耗费用与路程(单位：百公里)的平方成正比，比例系数为0.04，设该空载机的运输路程为百公里，则该空载机平均每一百公里的运输成本最低为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=x2+2ax-3与x轴交于A、B(1，0)两点(点A在点B的左侧)，与y轴交于点C，将抛物线沿y轴平移m(m＞0)个单位，当平移后的抛物线与线段OA有且只有一个交点时，则m的取值范围是_______________

    查看答案和解析>>

    同步练习册答案