
【题目】如图1,抛物线![]() :
:![]() 与直线l:
与直线l:![]() 交于x轴上的一点A,和另一点
交于x轴上的一点A,和另一点![]()
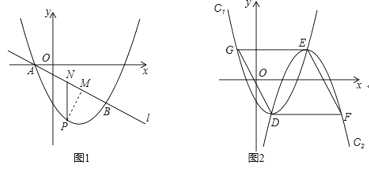
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
![]() 点P是抛物线
点P是抛物线![]() 上的一个动点
上的一个动点![]() 点P在A,B两点之间,但不包括A,B两点
点P在A,B两点之间,但不包括A,B两点![]() 于点M,
于点M,![]() 轴交AB于点N,求MN的最大值;
轴交AB于点N,求MN的最大值;
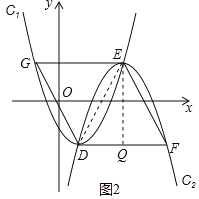
![]() 如图2,将抛物线
如图2,将抛物线![]() 绕顶点旋转
绕顶点旋转![]() 后,再作适当平移得到抛物线
后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第一象限的抛物线
的顶点E在第一象限的抛物线![]() 上,且抛持线
上,且抛持线![]() 与抛物线
与抛物线![]() 交于点D,过点D作
交于点D,过点D作![]() 轴交抛物线
轴交抛物线![]() 于点F,过点E作
于点F,过点E作![]() 轴交抛物线
轴交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点的横坐标为
点的横坐标为![]() 时,四边形DFEG为菱形
时,四边形DFEG为菱形
【解析】
![]() 求直线l与x轴交点A坐标、B坐标,用待定系数法求抛物线
求直线l与x轴交点A坐标、B坐标,用待定系数法求抛物线![]() 的解析式.
的解析式.
![]() 延长PN交x轴于点H,设点P横坐标为m,由
延长PN交x轴于点H,设点P横坐标为m,由![]() 轴可得点N、H横坐标也为m,即能用m表示PN、NH、AH的长.由
轴可得点N、H横坐标也为m,即能用m表示PN、NH、AH的长.由![]() 及对顶角
及对顶角![]() 可得
可得![]() 发现在
发现在![]() 中,MN与PN比值即为
中,MN与PN比值即为![]() ,故先在
,故先在![]() 中求
中求![]() 的值,再代入
的值,再代入![]() ,即得到MN与m的函数关系式,配方即求得MN最大值.
,即得到MN与m的函数关系式,配方即求得MN最大值.
![]() 设点
设点![]() ,所以可设抛物线
,所以可设抛物线![]() 顶点式为
顶点式为![]() 令两抛物线解析式
令两抛物线解析式![]() 列得关于x的方程,解得两抛物线的另一交点D即为抛物线
列得关于x的方程,解得两抛物线的另一交点D即为抛物线![]() 的顶点,故DG
的顶点,故DG![]() ,且求得DF平行且等于GE,即四边形DFEG首先一定是平行四边形.由DFEG为菱形可得
,且求得DF平行且等于GE,即四边形DFEG首先一定是平行四边形.由DFEG为菱形可得![]() ,故此时
,故此时![]() span>为等边三角形.利用特殊三角函数值作为等量关系列方程,即求得e的值.
span>为等边三角形.利用特殊三角函数值作为等量关系列方程,即求得e的值.
解:![]() 直线l:
直线l:![]() 交x轴于点A,
交x轴于点A,
![]() ,解得:
,解得:![]() ,
,
![]() ,
,
![]() 点
点![]() 在直线l上,
在直线l上,
![]() ,
,
![]() ,
,
![]() 抛物线
抛物线![]() :
:![]() 经过点A、B,
经过点A、B,
![]() ,
,
解得: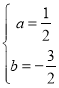 ,
,
![]() 抛物线
抛物线![]() 的解析式为
的解析式为![]() ,
,
![]() 如图1,延长PN交x轴于点H,
如图1,延长PN交x轴于点H,
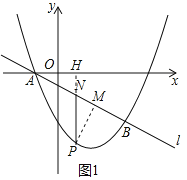
![]() ,
,
设![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
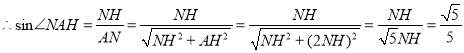 ,
,
![]() 于点M,
于点M,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 的最大值为
的最大值为![]() ,
,
![]() 存在满足条件的抛物线
存在满足条件的抛物线![]() ,使得四边形DFEG为菱形,
,使得四边形DFEG为菱形,
如图2,连接DE,过点E作![]() 于点Q,
于点Q,
![]() ,
,
![]() 抛物线
抛物线![]() 顶点为
顶点为![]() ,
,
设![]() ,
,
![]() 抛物线
抛物线![]() 顶点式为
顶点式为![]() ,
,
当![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 两抛物线另一交点
两抛物线另一交点![]() 为抛物线
为抛物线![]() 顶点,
顶点,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() 四边形DFEG是平行四边形,
四边形DFEG是平行四边形,
若DFEG为菱形,则![]() ,
,
![]() 由抛物线对称性可得:
由抛物线对称性可得:![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
解得:![]() 舍去
舍去![]() ,
,![]() ,
,
![]() 点的横坐标为
点的横坐标为![]() 时,四边形DFEG为菱形.
时,四边形DFEG为菱形.


科目:初中数学 来源: 题型:
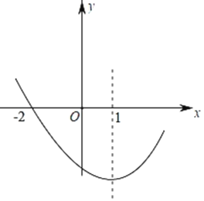
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如图不完整统计图.请结合图中信息,解决下列问题.
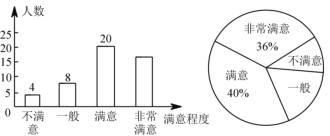
(1)此次调查中接受调查的人数为______人,其中“非常满意”的人数为______人;“一般”部分所在扇形统计图的圆心角度数为_______.
(2)兴趣小组准备从“不满意”的![]() 位群众中随机选择
位群众中随机选择![]() 位进行回访,已知这
位进行回访,已知这![]() 位群众中有
位群众中有![]() 位来自甲片区,另
位来自甲片区,另![]() 位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
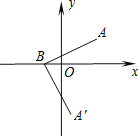
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和图形
和图形![]() ,给出如下定义:若图形
,给出如下定义:若图形![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 是边长为2的等边三角形,则称点
是边长为2的等边三角形,则称点![]() 是图形
是图形![]() 的一个“和谐点”.
的一个“和谐点”.
已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 的半径为
的半径为![]() .
.
(1)若![]() ,在点
,在点![]() 中,直线
中,直线![]() 的和谐点是___________;
的和谐点是___________;
(2)若![]() 上恰好存在2个直线
上恰好存在2个直线![]() 的和谐点,求
的和谐点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,线段
,线段![]() 上存在
上存在![]() 的和谐点,直接写出
的和谐点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com