
����Ŀ������֪����һԪ���η���x2=��1û��ʵ��������������һ��ʵ����ƽ�����ک�1�������ǹ涨һ��������i����ʹ������i2=��1��������x2=��1��һ����Ϊi�������ҽ�һ���涨��һ��ʵ�����������������������㣬��ԭ�������ɺ����㷨����Ȼ������������i1=i��i2=��1��i3=i2i=����1��i=��i��i4=��i2��2=����1��2=1���Ӷ���������������n�����ǿ��Եõ�i4n+1=i4ni=��i4��ni=i��ͬ���ɵ�i4n+2=��1��i4n+3=��i��i4n=1����ôi+i2+i3+i4+��+i2012+i2013��ֵΪ��������
A. 0 B. i C. ��1 D. 1

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��kx��b��ͼ����(��2��4)����������������y��2x��ͼ��ƽ�У�
(1) ��һ�κ���y��kx��b�Ľ���ʽ��
(2) ��һ�κ���y��kx��b��ͼ������������Χ�ɵ������ε������
(3) ��A(a��y1)��B(a��b��y2)Ϊһ�κ���y��kx��b��ͼ���������㣬�ԱȽ�y1��y2�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������п�ǰ�����������˾��꼶ѧ���ġ�1�����������ɼ��������Ƴ��������Ƶ���ֲ�ֱ��ͼ��ÿС�麬��Сֵ���������ֵ��������ͼ�� 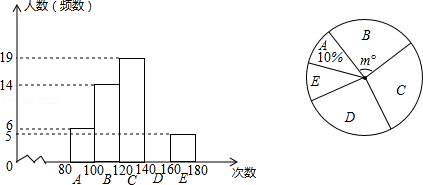
��1����ȫƵ���ֲ�ֱ��ͼ��
��2������ͼ��m=��
��3������1�����������ɼ����ڻ����140��Ϊ���㣬�����ȫ�о��꼶5900��ѧ���С�1�����������ɼ�Ϊ����Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��AB��O������BOD=40�㣬����ȷ�Ľ����ǣ� ��

A����AOC=40�� B����COE=130�� C����EOD=40�� D����BOE=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
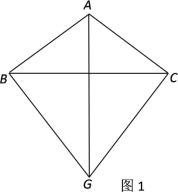
����Ŀ����ͼ1������ABC�У�AB��AC��GΪ��������һ�㣬����GBCΪ�ȱ������Σ�
��1����֤��ֱ��AG��ֱƽ��BC��
��2����ABΪһ�����ȱ���ABE����ͼ2��������EG��EC�����ж���EGC�Ƿ�ֱ�������Σ���˵�����ɣ�
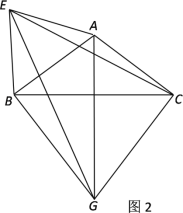
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ����������A��1����1����B����1����1����C��0��1������P��0��2������A�ĶԳƵ�ΪP1��P1����B�ĶԳƵ�ΪP2��P2����C�ĶԳƵ�ΪP3�����˹��ɼ�����A��B��CΪ�Գ������ظ�ǰ��IJ��������εõ�P4��P5��P6���������P2018��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�Ȼ�����������⣮
����֪������2x+3y=12��������⣬����ʵ����������������ֻ��Ҫ������������⣮������2x+3y=12����![]() ����x��yΪ����������
����x��y����������![]() ����0��x��6����
����0��x��6����![]() ����������
����������![]() ��������
��������
��2��3���ʣ���֪��xΪ3�ı������Ӷ�x=3������![]() =2��
=2��
��2x+3y=12����������Ϊ![]()
���⣺
��1������д������2x+y=5��һ���������⣺_____��
��2����![]() Ϊ��Ȼ��������������������xֵ��_____����
Ϊ��Ȼ��������������������xֵ��_____����
A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����

��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
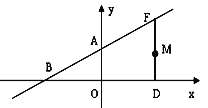
����Ŀ����ͼ��һ�κ���![]() ��ͼ��y���ڵ�A����x���ڵ�B����F������BA�ϣ�����F��x��Ĵ��ߣ���DΪ���㣬
��ͼ��y���ڵ�A����x���ڵ�B����F������BA�ϣ�����F��x��Ĵ��ߣ���DΪ���㣬
����OD=6����F������ꣻ
(2)��OD=12��M���߶�FD�ϣ�M��������Ϊm������BM���ú���m�Ĵ���ʽ��ʾ��BMF�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com