
小明遇到这样一个问题:“如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.”
分析时,小明发现,分别延长QE,MF,NG,PH交FA,GB,HC,ED的延长线于 点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个正方形(无缝隙不重叠),则这个正方形的边长为_______
(2)求正方形MNPQ的面积.
(3)参考小明思 考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ.若S△RPQ= ,则AD的长为_______.
,则AD的长为_______.

(1) a;(2)2;(3)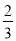 .
.
【解析】
试题分析:(1)四个等腰直角三角形的斜边长为a,其拼成的正方形的面积为a2;
(2)如图2所示,正方形MNPQ的面积等于四个虚线小等腰直角三角形的面积之和,据此求出正方形MNPQ的面积;
(3)参照小明的钥匙思路,对问题作同样的等积变形,即可求解问题.
(1) a
(2) ∵四个等腰直角三角形△RQF,△SMG,△TNH,△WPE的面积和为a2,正方形ABCD的面积为a2,
∴S正方形MNPQ=S△ARE+S△DWH+S△GCT+S△SBF=4S△ARE=4×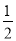 ×12=2;
×12=2;
(3)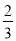
如答图1所示,分别延长RD,QF,PE,
交FA,EC,DB的延长线于点S,T,W.

由题意易得:△RSF,△QET,△PDW均为底角是30°的等腰三角形,其底边长均等于△ABC的边长.
所以△RSF,△QET,△PDW的面积等于△ABC的面积。
由此可得:S△RPQ=S△ADS+S△CFT+S△BEW=3S△ADS,
过点A作AN⊥SD于点N,设AD=AS=x,
则AN=AD•sin30°=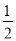 x,SD=2ND=2ADcos30°=
x,SD=2ND=2ADcos30°=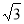 x,
x,
∴S△ADS=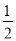 SD•AN=
SD•AN=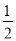 •
•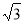 x•
x•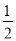 x=
x=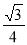 x2.
x2.
∴S△RPQ=S△ADS+S△CFT+S△BEW=3S△ADS,
∴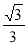 =3×
=3× x2,得x2=
x2,得x2=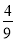 ,
,
解得x=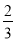 或x=?
或x=?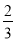 (不合题意,舍去)
(不合题意,舍去)
∴x=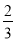 ,即AD的长为
,即AD的长为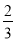 。
。
考点: 四边形综合题.


科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:解答题
如图1,在平面直角坐标系中,点A、C分别在y轴和x轴上,AB∥x轴,sinC= ,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从 点C出发,以1cm/s的速度沿边 CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点 P 运动的时间为t (s),△CPQ 的面积为 S(cm2), 已知S与t之间的函数关系如图2中曲线段 OE、线段 EF与曲线段FG 给出.
,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从 点C出发,以1cm/s的速度沿边 CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点 P 运动的时间为t (s),△CPQ 的面积为 S(cm2), 已知S与t之间的函数关系如图2中曲线段 OE、线段 EF与曲线段FG 给出.
(1)点P的运动速度为 cm/s, 点B、C的坐标分别为 , ;
(2)求曲线FG段的函数解析式;
(3)当t为何值时,△CPQ 的面积是四边形OABC的面积的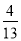 ?
?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2 cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为( )

A.6 cm2 B.3 cm2 C.(2+π)cm2 D.(6-π)cm2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
方程 -
- =0的解为( )
=0的解为( )
A.x=2 B.x=-2 C.x=3 D.x=-3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:填空题
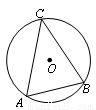
如图,⊙O的半径为4,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com