
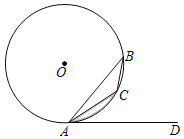
【题目】如图,直线AD经过⊙O上的点A,△ABC为⊙O的内接三角形,并且∠CAD=∠B.
(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若∠CAD=30°,⊙O的半径为1,求图中阴影部分的面积.(结果保留π)
【答案】(1)直线AD与⊙O的位置关系是相切,理由见解析;(2)![]()
【解析】
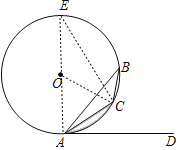
(1)作直径AE,连接CE,求出∠OAD=90°,根据切线的判定得出即可;
(2)求出△OAC是等边三角形,再分别求出△OAC和扇形OCA的面积,即可得出答案.
(1)直线AD与⊙O的位置关系是相切,
理由是:作直径AE,连接CE,
∵AE为直径,
∴∠ACE=90°,
∴∠E+∠EAC=90°,
∵∠B=∠DAC,∠B=∠E,
∴∠E=∠DAC,
∴∠EAC+∠DAC=90°,
即OA⊥AD,
∵OA过O,
∴直线AD与⊙O的位置关系是相切;
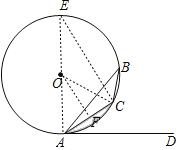
(2)连接OC,过O作OF⊥AC于F,则∠OFA=90,
∵∠CAD=30°,∠DAO=90°,
∴∠OAC=60°,
∵OC=OA=1,
∴△OAC是等边三角形,
∴AC=OA=1,∠AOC=60°,
∵OA=OC,OF⊥AC,
∴AF=FC=![]() ,
,
由勾股定理得:OF=![]() ,
,
∴阴影部分的面积为:![]()


科目:初中数学 来源: 题型:
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了 50 件产品并对某一项关键质量指标做检测,获得了它们的质量指标值 s ,并对样本数据(质量指标值 s )进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 | 20 ≤ s 25 | 25 ≤ s 30 | 30 ≤ s 35 | 35 ≤ s 40 | 40 ≤ s ≤ 45 |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀); 等级是次品为质量不合格.
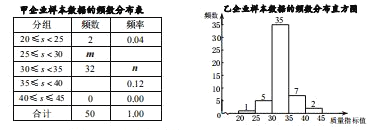
b.甲企业样本数据的频数分布统计表如下(不完整):
c.乙企业样本数据的频数分布直方图如下:
d.两企业样本数据的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 15.34 |
根据以上信息,回答下列问题:
(1) m 的值为 , n 的值为 ;
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为 ; 若乙企业生产的某批产品共5 万件,估计质量优秀的有 万件;
(3)根据图表数据,你认为 企业生产的产品质量较好,理由为 .(从某个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
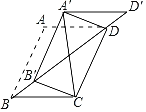
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;…,如此进行下去,直至得
;…,如此进行下去,直至得![]() .
.
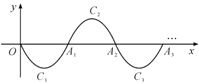
(1)请写出抛物线![]() 的解析式:________;
的解析式:________;
(2)若![]() 在第10段抛物线
在第10段抛物线![]() 上,则
上,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知,AB=AC=6,BC=10.E是C边上一动点(E不与点B、C重合),△DEF≌△ABC.其中点A,B的对应点分别是点D、E,且点E在运动时,DE边始终经过点A,设EF与AC相交于点G,当△AEG为等腰三角形时,则BE的长为_____.
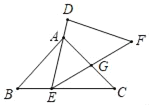
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
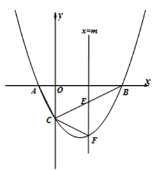
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com