


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
 已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,甲船以5海里/小时的速度离开港口O沿南偏东30°方向航行,乙船同时同地沿某方向以12海里/小时的速度航行,已知它们离开港口2小时后分别到达B、A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗?
如图所示,甲船以5海里/小时的速度离开港口O沿南偏东30°方向航行,乙船同时同地沿某方向以12海里/小时的速度航行,已知它们离开港口2小时后分别到达B、A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
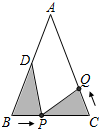 如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为
如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com