
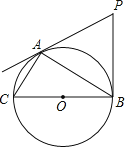
【题目】如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() 米,
米,![]() 米,
米,![]() 点位于
点位于![]() 点的南偏西
点的南偏西![]() 方向,
方向,![]() 点位于
点位于![]() 点的南偏东
点的南偏东![]() 方向.
方向.
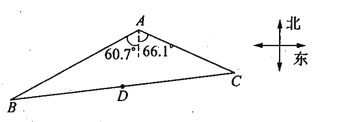
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0.1米)
间的距离.(结果精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的网格中,每个小方格都是边长为1的正方形,B点的坐标为(-1,-1).
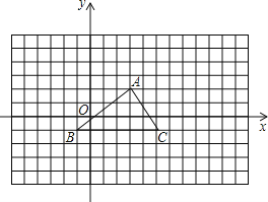
(1)把格点△ABC绕点B按逆时针方向旋转90°后得到△A1BC1,请画出△A1BC1,并写出点A1的坐标;
(2)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的相似之比为1:2,请在下面网格内画出△AB2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
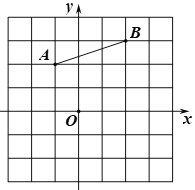
【题目】如图,在直角坐标系中,线段AB的两个端点坐标分别为(﹣1,2),(2,3),把线段AB绕着原点O顺时针旋转90°得到线段A'B',点A的对应点为A'.
(1)画出线段A'B',并写出点A',B'的坐标;
(2)根据(1)中的变化规律,把OM绕着原点O顺时针旋转90°得到ON,则点M(m,n)的对应点N的坐标是( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
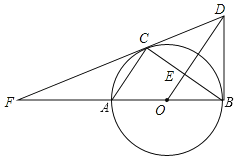
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
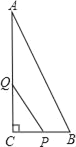
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
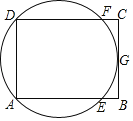
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
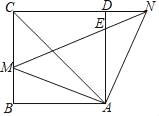
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电台“市民热线”对上周内接到的热线电话进行了分类统计,得到的统计信息图如图所示,其中有关房产城建的电话有30个,请你根据统计图的信息回答以下问题:
(1)道路交通热线电话是多少个占总数百分比是多少?
(2)上周“市民热线”接到有关环境保护方面的电话有多少个?
(3)据此估计,除环境保护方面的电话外,“市民热线”今年(按52周计算)将接到的热线电话约多少个?
(4)为了更直观显示各类“市民热线”电话的数目,你准备采用什么样的统计方法?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com