
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长与
并延长与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
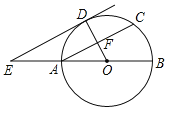
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,请求出四边形
,请求出四边形![]() 的面积。
的面积。
【答案】(1)见解析;(2)18![]() .
.
【解析】
(1)根据垂弦定理可得OD⊥AC,根据切线的定义可得OD⊥DE,根据平行线的性质即可解答;
(2)连接CD,根据AC∥DE,OA=AE,可得点F是OD的中点,然后可得![]() AFO≌
AFO≌![]() CFD(SAS),所以S△AFO=S△CFD,通过等量代换可得S四边形ACDE=S△ODE即可解答.
CFD(SAS),所以S△AFO=S△CFD,通过等量代换可得S四边形ACDE=S△ODE即可解答.
解:(1)证明:∵F为弦AC的中点,∴OD⊥AC,
∵DE切⊙O于点D,∴OD⊥DE,∴AC∥DE;
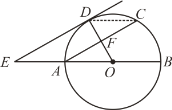
(2)如图,连接CD,
∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,
又∵AF=CF,∠AFO=∠CFD,
∴![]() AFO≌
AFO≌![]() CFD(SAS),
CFD(SAS),
∴S△AFO=S△CFD,∴S四边形ACDE=S△ODE,
在Rt△ODE中,OD=OA=AE=6,∴OE=12,
∴DE=![]() =
=![]() =6
=6![]() ,
,
∴S四边形ACDE=S△ODE=![]() ×OD×DE=
×OD×DE=![]() ×6×6
×6×6![]() =18
=18![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
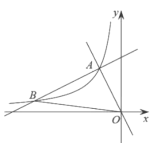
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
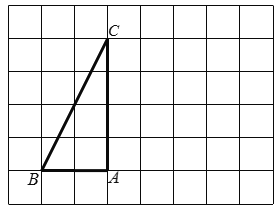
【题目】如图,在每个小正方形的边长为![]() 的网格中,△
的网格中,△![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(1)![]() 的长等于_____________;
的长等于_____________;
(2)在如图所示的网格中,将△![]() 绕点
绕点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,得到△
上,得到△![]() ,请用无刻度的直尺,画出△
,请用无刻度的直尺,画出△![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 对折,得到
对折,得到![]() ,延长
,延长![]() 交
交![]() 延长线于点
延长线于点![]() ,下列4个结论:①
,下列4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;正确的结论有__________
;正确的结论有__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期复学后,学校为了保障学生的出行安全,随机调查了部分学生的上学方式(每位学生从乘私家车、坐公交、骑车和步行4种方式中限选1项),根据调查数据制作了如图所示的不完整的统计表和扇形统计图.

(1)本次学校共调查了 名学生,![]() ,
,![]() ;
;
(2)求扇形统计图中“步行”对应扇形的圆心角;
(3)甲、乙两位同学住在同一小区,且都坐公交车上学,有![]() 、
、![]() 、
、![]() 三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
三路公交车途径该小区和学校,假设甲、乙两位同学坐这三路公交车是等可能的,请用列表或画树状图的方法求某日甲、乙两位同学坐同一路公交车到学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,正方形![]() 与正方形
与正方形![]() 有公共的顶点
有公共的顶点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
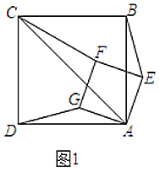
①求证:![]() ;
;
②求![]() 的值;
的值;
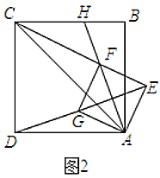
(2)将图1中的正方形![]() 旋转到图2的位置,当
旋转到图2的位置,当![]() ,
,![]() ,
,![]() 在一条直线上,若
在一条直线上,若![]() ,求正方形
,求正方形![]() 的边长.
的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com