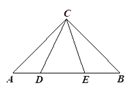
【题目】如图，
,
,
，如果
，则
的长是( )．
A. 
B. 
C. 
D. 
【答案】C
【解析】分析：由于△ABC中，AC=BC，∠ACB=90°，设DE=x，则AB=7+x，可以得出△ACE∽△CDE∽△BDC，根据相似三角形的性质，列出关于x方程，解出x，再计算BC的长．
详解：设DE=x，则AB=7+x．
∵∠ACB=90°，AC=BC，∴∠DCE=∠CAE=∠DBC=45°
∴△ACE∽△CDE∽△BDC，设CD=a，CE=b，则有以下等式：
x：b=b：3+x，x：a=a：4+x，x：a=b：AC，
整理得：b2=x（x+3），a2=x（x+4），xAC=ab，
x2（x+3）（x+4）=a2b2=x2AC2=
，
解得：x=5；
∴AB=12，∴AC=BC=6
．
故选C．
科目：初中数学 来源： 题型：
【题目】7 月 9 日，滴滴发布北京市滴滴网约车价格调整，公布了新的滴滴快车计价规则，车费由“总里程费＋总时长费”两部分构成，不同时段收费标准不同，具体收费标准如下表，如果车费不足起步价，则按起步价收费.
时间段 | 里程费（元/千米） | 时长费（元/分钟） | 起步价（元） |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 2.15 | 0.80 | 14.00 |
(1)小明早上 7:10 乘坐滴滴快车上学，行车里程 6 千米，行车时间 10 分钟，则应付车费多少元?
(2)小云 17:10 放学回家，行车里程 1 千米，行车时间 15 分钟，则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家，20:45 在学校上车，由于堵车，平均速度是 a 千米/小时，15 分钟后走另外一条路回家，平均速度是 b 千米/小时，5 分钟后到家，则他应付车费多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为引导学生广泛阅读文学名著，某校在七年级、八年级开展了读书知识竞赛．该校七、八年级各有学生400人，各随机抽取20名学生进行了抽样调查，获得了他们知识竞赛成绩（分），并对数据进行整理、描述和分析．下面给出了部分信息．
七年级：
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年级：
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
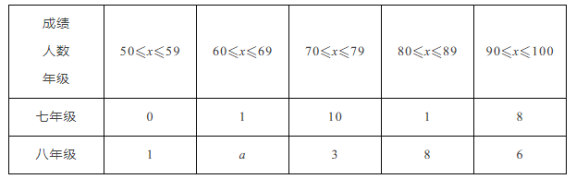
平均数、中位数、众数如表所示：
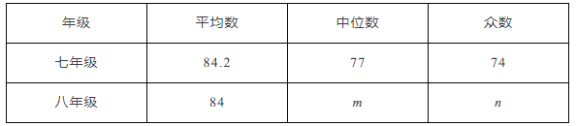
根据以上信息，回答下列问题：
（1）
______，
______，
______；
（2）该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号，请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人；
（3）结合以上数据，你认为哪个年级读书知识竞赛的总体成绩较好，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，平行四边形ABCD在平面直角坐标系中，A、B（点A在点B的左侧）两点的横坐标是方程
的两个根，点D在y轴上其中
．
（1）求平行四边形ABCD的面积；
（2）若P是第一象限位于直线BD上方的一点，过P作
于E，过E作
轴于H点，作PF∥y轴交直线BD于F，F为BD中点，其中△PEF的周长是
；若M为线段AD上一动点，N为直线BD上一动点，连接HN，NM，求
的最小值，此时y轴上有一个动点G，当
最大时，求G点坐标；
（3）在（2）的情况下，将△AOD绕O点逆时针旋转60°后得到
如图2，将线段
沿着x轴平移，记平移过程中的线段为
，在平面直角坐标系中是否存在点S，使得以点
，
，E，S为顶点的四边形为菱形，若存在，请求出点S的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．
（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4
，求四边形AEDF的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知代数式A＝x2+xy+2y－1，B＝2x2－xy
(1)若(x+1)2+|y－2|＝0，求2A－B的值；
(2)若2A－B的值与y的取值无关，求x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某出租车一天下午某时间段以广场为出发点，在东西方向的大道上营运，规定向东为正，向西为负，单次行车里程依先后顺序记录如下：（单位：
）+9，-3，-5，+4，-8，+7，-2，-5，+8，-4
（1）该出租车司机将最后一名乘客送到目的地后，出租车在广场的什么方向？距广场多远？
（2）若每千米耗油0.08升，该出租车这个时间段共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次为地震灾区的捐款活动中，某校随机调查了50名学生的捐款情况，统计如表：
捐款金额（元） | 5 | 10 | 15 | 20 | 50 |
捐款人数（人） | 7 | 18 | 10 | 12 | 3 |
（1）这50名学生捐款金额的众数和中位数分别为多少元？
（2）如果把这50名学生的捐款情况绘制成扇形统计图，则捐款金额为15元的人数所对应的扇形圆心角为多少度？
（3）若该校共有1200名学生，估计该校的捐款总数大约是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9．其中说法正确的结论有______________
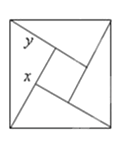
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com