
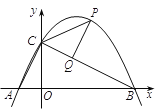
【题目】如图,二次函数y=ax2+bx+2![]() 的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
⑴ 求该二次函数的表达式;
⑵ P是该函数在第一象限内图像上的动点,过点P作PQ⊥BC于点Q,连接PC、AC.
① 求线段PQ的最大值;
② 若以点P、C、Q为顶点的三角形与△ACO相似,求P点的坐标.
【答案】(1)![]() ;(2)①PQ的最大值=
;(2)①PQ的最大值= ![]() ,② P点的坐标为:P1(4,2
,② P点的坐标为:P1(4,2![]() ),P2
),P2 ![]()
【解析】分析:(1)把点A,B的坐标代入到二次函数的解析式中求解;(2)过点P作PD⊥x轴于点N交BC于点M,P点坐标为![]() ,用t表示出点M,根据二次函数的性质求PM的最大值,再结合三角形相似求PQ的最大值;(3)分两种情况画出图形,根据平行线或相似三角形求解.
,用t表示出点M,根据二次函数的性质求PM的最大值,再结合三角形相似求PQ的最大值;(3)分两种情况画出图形,根据平行线或相似三角形求解.
详解:⑴∵y=ax2+bx+![]() 的图像过点A(-2,0),B(6,0).
的图像过点A(-2,0),B(6,0).
∴![]() 解之得:
解之得: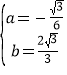 ;
;
∴所求二次函数的表达式为:![]() .
.
⑵①设P点坐标为:![]() ,且0<t<6,
,且0<t<6,
令x=0,则y=4,∴C(0,2![]() ).
).
设BC的表达式为:
y=mx+n(m≠0)过B(6,0),C(0,![]() ),
),
![]() ,解之得:
,解之得: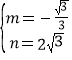 ,∴BC的表达式为:
,∴BC的表达式为:![]() ,
,
过点P作PD⊥x轴于点N交BC于点M,(如图1)
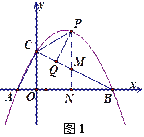
∴点M的横坐标为t,∴它的纵坐标为![]() ,
,
∴M![]() .
.
PM=yP-yM=![]() ,
,
∵x轴⊥y轴,PQ⊥BC,PD⊥x轴.
∴∠AOC=∠COB=∠CQP=∠PQM=∠MDB=90°,
又∵AO=2,OB=8,CO=4,
∴![]() ,∴△OAC∽△OCB,∴∠ACO=∠CBO=∠MPQ,
,∴△OAC∽△OCB,∴∠ACO=∠CBO=∠MPQ,
∴△OAC∽△OCB∽△DMB∽△QMP.
∵![]() ,
,
∴cos∠MPQ=cos∠ACO=![]() .
.
∵cos∠MPQ=![]() ,
,
∴![]() .
.
∵a<0,且t=3的值在0<t<6的范围内,
∴当t=3时,PQ的最大值=![]() .
.
②(ⅰ)当△QPC∽△OAC时,(如图2)
则∠ACO=∠CBA=∠PCQ,
∴PC∥x轴,
由抛物线的对称性知:点C与点P关于抛物线的对称轴对称,
∴P点的坐标为(4,![]() ).
).
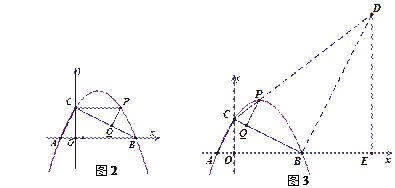
(ⅱ)当△QCP∽△OAC时,(如图3)
则∠CAO=∠PCQ,
∴tan∠CAO=tan∠PCQ,
过点B作BD⊥BC交CP的延长线于点D,
再过点D作DE⊥x轴于点E,
则△OBC∽△EDB,
∴![]() ,
,
∴BE=![]() CO=
CO=![]() ×2
×2![]() =6,∴OE=OB+BE=12,
=6,∴OE=OB+BE=12,
DE=![]() BO=
BO=![]() ×6=6
×6=6![]() ,∴点D的坐标为(12,6
,∴点D的坐标为(12,6![]() ).
).
设直线CD的表达式为y=ex+f,且过点C(0,![]() ),D(12,6
),D(12,6![]() ),
),
∴![]() ,解得,
,解得,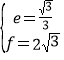 .
.
∴直线CD的表达式为:![]() ,
,
∴P坐标是方程组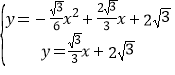 的解,
的解,
解之得: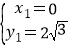 (舍),
(舍),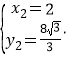
∴点P的坐标为(![]() ).
).
综上所述:P点的坐标为:P1(4,![]() ),P2(
),P2(![]() ).
).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,今年水果总产量为18000 千克,此水果在市场上每千克售 a 元,在果园每千克售b 元( b a ),该农户将水果拉到市场出售平均每天出售1000 千克,需8 人帮忙,每人每天付工资 25 元,农用车运费及其他各项税费平均每天100 元.
(1)分别用 a,b 表示两种方式出售水果的收入;
(2)若 a1.3元, b1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
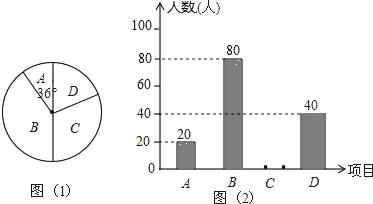
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院,B.小小数学家,C.小小外交家,D.未来科学家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好同时选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
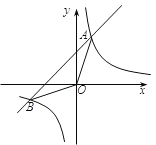
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点A(1,3),B(n,-1).
的图像交于两点A(1,3),B(n,-1).
⑴ k= ,n= ;
⑵ 求一次函数的表达式;
⑶ 结合图像直接回答:不等式![]() <mx+b解集是 ;
<mx+b解集是 ;
⑷ 求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
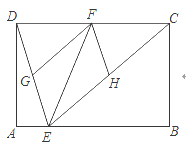
【题目】如图,已知矩形ABCD中,点E是AB边上的一个动点,点F、G、H分别是CD、DE、CE的中点.
(1)求证:四边形EHFG是平行四边形;
(2)设AB=4,AD=3,求△EFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
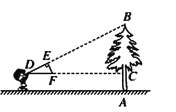
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
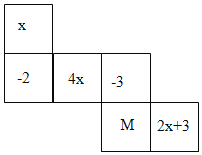
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com