
【题目】如图,己知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,
,![]() 为
为![]() 垂直平分线,且
垂直平分线,且![]() ,连接
,连接![]() ,
,![]() .
.

(1)直接写出![]() __________,
__________,![]() __________;
__________;
(2)求证:![]() 是等边三角形;
是等边三角形;
(3)如图,连接![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,直接写出
,直接写出![]() 的长;
的长;


(4)![]() 是直线
是直线![]() 上的一点,且
上的一点,且![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】(1)![]() ,
,![]() (2)证明见解析(3)
(2)证明见解析(3)![]() (4)
(4)![]() 或
或![]()
【解析】
(1)根据含有30°角的直角三角形的性质可得BC=2,再由勾股定理即可求出AC的长;
(2)由![]() 为
为![]() 垂直平分线可得DB=DA,在Rt△BDE中,由勾股定理可得BD=4,可得BD=2BE,故∠BDE为60°,即可证明
垂直平分线可得DB=DA,在Rt△BDE中,由勾股定理可得BD=4,可得BD=2BE,故∠BDE为60°,即可证明![]() 是等边三角形;
是等边三角形;
(3)由(1)(2)可知,![]() ,AD=4,进而可求得CD的长,再由等积法可得
,AD=4,进而可求得CD的长,再由等积法可得![]() ,代入求解即可;
,代入求解即可;
(4)分点P在线段AC上和AC的延长线上两种情况,过点E作AC的垂线交AC于点Q,构造Rt△PQE,再根据勾股定理即可求解.
(1)∵![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)∵![]() 为
为![]() 垂直平分线,∴ADB=DA,
垂直平分线,∴ADB=DA,
在Rt△BDE中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴BD=2BE,∴∠BDE为60°,
∴![]() 为等边三角形;
为等边三角形;
(3))由(1)(2)可知,![]() ,AD=4,
,AD=4,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(4)分点P在线段AC上和AC的延长线上两种情况,
如图,过点E作AC的垂线交AC于点Q,
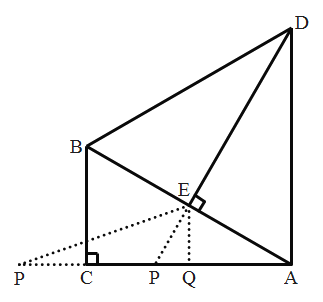
∵AE=2,∠BAC=30°,∴EQ=1,
∵![]() ,∴
,∴![]() ,
,
①若点P在线段AC上,
则![]() ,
,
∴![]() ;
;
②若点P在线段AC的延长线上,
则![]() ,
,
∴![]() ;
;
综上,PE的长为![]() 或
或![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,且
,且![]() .
.

![]() 如图,若
如图,若![]() 点恰好是抛物线的顶点,请写出它的对称轴和
点恰好是抛物线的顶点,请写出它的对称轴和![]() 的值.
的值.
![]() 若
若![]() ,求
,求![]() 、
、![]() 的值,并指出此时抛物线的开口方向.
的值,并指出此时抛物线的开口方向.
![]() 若抛物线
若抛物线![]() 的开口向下,请直接写出
的开口向下,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④![]() <0,其中正确的结论是_____.
<0,其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市.张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施.已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
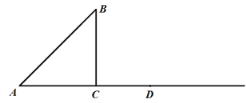
【题目】已知:![]() 点D是AC延长线上一点,且
点D是AC延长线上一点,且![]() ,M是线段CD上一个动点,连接BM,延长MB到H,使得
,M是线段CD上一个动点,连接BM,延长MB到H,使得![]() 以点B为中心,将线段BH逆时针旋转
以点B为中心,将线段BH逆时针旋转![]() 得到线段BQ,连接AQ.
得到线段BQ,连接AQ.
(1)依题意补全图形;
(2)求证:![]()
(3)点N是射线AC上一点,且点N是点M关于点D的对称点,连接BN,如果![]() 求线段AB的长.
求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com