
【题目】已知Rt△ABC,∠BAC=90°,点D是BC中点,AD=AC,BC=4![]() ,过A,D两点作⊙O,交AB于点E,
,过A,D两点作⊙O,交AB于点E,
(1)求弦AD的长;
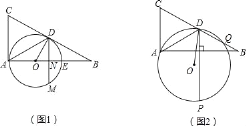
(2)如图1,当圆心O在AB上且点M是⊙O上一动点,连接DM交AB于点N,求当ON等于多少时,三点D、E、M组成的三角形是等腰三角形?
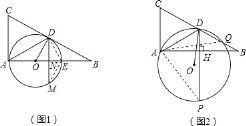
(3)如图2,当圆心O不在AB上且动圆⊙O与DB相交于点Q时,过D作DH⊥AB(垂足为H)并交⊙O于点P,问:当⊙O变动时DP﹣DQ的值变不变?若不变,请求出其值;若变化,请说明理由.
【答案】(1)![]()
(2)当ON等于1或![]() ﹣1时,三点D、E、M组成的三角形是等腰三角形
﹣1时,三点D、E、M组成的三角形是等腰三角形
(3)不变,理由见解析
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半即可得到AD的长;
(2)连DE、ME,易得当ED和EM为等腰三角形EDM的两腰,根据垂径定理得推论得OE⊥DM,易得到△ADC为等边三角形,得∠CAD=60°,则∠DAO=30°,∠DON=60°,然后根据含30°的直角三角形三边的关系得DN=![]() AD=
AD=![]() ,ON=
,ON=![]() DN=1;
DN=1;
当MD=ME,DE为底边,作DH⊥AE,由于AD=2![]() ,∠DAE=30°,得到DH=
,∠DAE=30°,得到DH=![]() ,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
又∠M=∠DAE=30°,MD=ME,得到∠MDE=75°,则∠ADM=90°-75°=15°,可得到∠DNO=45°,根据等腰直角三角形的性质得到NH=DH=![]() ,则ON=
,则ON=![]() -1;
-1;
(3)连AP、AQ,DP⊥AB,得AC∥DP,则∠PDB=∠C=60°,再根据圆周角定理得∠PAQ=∠PDB,∠AQC=∠P,则∠PAQ=60°,∠CAQ=∠PAD,易证得△AQC≌△APD,得到
DP=CQ,则DP-DQ=CQ-DQ=CD,而△ADC为等边三角形,CD=AD=2![]() ,即可得到DP-DQ的值.
,即可得到DP-DQ的值.
解:(1)∵∠BAC=90°,点D是BC中点,BC=4![]() ,
,
∴AD=![]() BC=
BC=![]() ;
;
(2)连DE、ME,如图,∵DM>DE,
当ED和EM为等腰三角形EDM的两腰,
∴OE⊥DM,
又∵AD=AC,
∴△ADC为等边三角形,
∴∠CAD=60°,
∴∠DAO=30°,
∴∠DON=60°,
在Rt△ADN中,DN=![]() AD=
AD=![]() ,
,
在Rt△ODN中,ON=![]() DN=1,
DN=1,
∴当ON等于1时,三点D、E、M组成的三角形是等腰三角形;
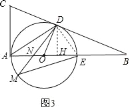
当MD=ME,DE为底边,如图3,作DH⊥AE,
∵AD=2![]() ,∠DAE=30°,
,∠DAE=30°,
∴DH=![]() ,∠DEA=60°,DE=2,
,∠DEA=60°,DE=2,
∴△ODE为等边三角形,
∴OE=DE=2,OH=1,
∵∠M=∠DAE=30°,
而MD=ME,
∴∠MDE=75°,
∴∠ADM=90°﹣75°=15°,
∴∠DNO=45°,
∴△NDH为等腰直角三角形,
∴NH=DH=![]() ,
,
∴ON=![]() ﹣1;
﹣1;
综上所述,当ON等于1或![]() ﹣1时,三点D、E、M组成的三角形是等腰三角形;
﹣1时,三点D、E、M组成的三角形是等腰三角形;
(3)当⊙O变动时DP﹣DQ的值不变,DP﹣DQ=2![]() .理由如下:
.理由如下:
连AP、AQ,如图2,
∵∠C=∠CAD=60°,
而DP⊥AB,
∴AC∥DP,
∴∠PDB=∠C=60°,
又∵∠PAQ=∠PDB,
∴∠PAQ=60°,
∴∠CAQ=∠PAD,
∵AC=AD,∠AQC=∠P,
∴△AQC≌△APD,
∴DP=CQ,
∴DP﹣DQ=CQ﹣DQ=CD=2![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
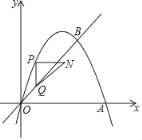
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,且不与点O、B重合,过点P作y轴的平行线交射线OB于点Q,以PQ为边作R△PQN,点N与点B始终在PQ同侧,且PN=1.设点P的横坐标为m(m>0),PQ长度为d.
(1)用含m的代数式表示点P的坐标.
(2)求d与m之间的函数关系式.
(3)当△PQN是等腰直角三角形时,求m的值.
(4)直接写出△PQN的边与抛物线有两个交点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
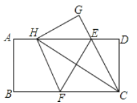
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
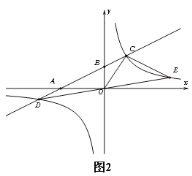
【题目】如图1,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于C(2,n)、D两点,与x轴,y轴分别交于A、B(0,2)两点,如果△AOC的面积为6.
的图象交于C(2,n)、D两点,与x轴,y轴分别交于A、B(0,2)两点,如果△AOC的面积为6.
(1)求点A的坐标
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和△COE的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,我市为了解学生的视力变化情况,从全市八年级随机抽取了1200名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.

解答下列问题:
(1)图中“其他”所在扇形的圆心角度数为 ;
(2)若2016年全市八年级学生共有24000名,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你认为造成中学生视力下降最主要的因素是什么,你觉得中学生应该如何保护视力?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
, ![]() 上,将纸片
上,将纸片![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在
落在![]() 上的一点
上的一点![]() 处,点
处,点![]() 落在点
落在点![]() 处,有以下四个结论:
处,有以下四个结论:
①四边形![]() 是菱形;②
是菱形;②![]() 平分
平分![]() ;③线段
;③线段![]() 的取值范围为
的取值范围为![]() ;④当点
;④当点![]() 与点
与点![]() 重合时,
重合时,![]() .
.
以上结论中,你认为正确的有( )个.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
小明从中任意选取一个结论,则选中正确结论的概率为( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
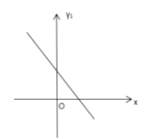
【题目】在平面直角坐标系中,函数y1=ax+b(a、b为常数,且ab≠0)的图象如图所示,y2=bx+a,设y=y1·y2.
(1)当b=-2a时,
①若点(1,4)在函数y的图象上,求函数y的表达式;
②若点(x1,p)和(x2,q)在函数y的图象上,且![]() ,比较p,q的大小;
,比较p,q的大小;
(2)若函数y的图象与x轴交于(m,0)和(n,0)两点,求证:m=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
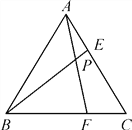
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com