
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
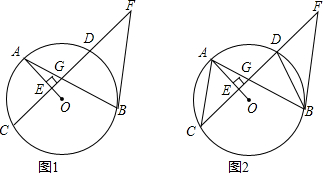
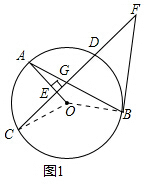 证明:(1)如图1,连接OB,
证明:(1)如图1,连接OB,| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| AE |
| CE |
| 3 |
| 4 |
| AE | ||
|
| 3 |
| 4 |
| 3 |
| 8 |
| 1 |
| 4 |
| 3 |
| 8 |
| 25 |
| 48 |
| 25 |
| 48 |


科目:初中数学 来源: 题型:
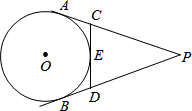 如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )| A、15 | B、12 | C、20 | D、30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1000件 |
| B、1200件 |
| C、2000件 |
| D、10000件 |
查看答案和解析>>
科目:初中数学 来源: 题型:
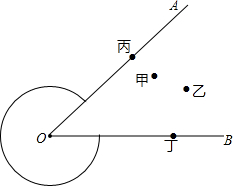 甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写)
甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com