
【题目】已知:如图,在△ABC中,AB=13,AC=20,BC=21,AD⊥BC,垂足为点D.
(1)求BD、CD的长;
(2)求△ABC的面积.

【答案】(1)BD=5,CD=16;(2)126
【解析】
(1)设BD=x,则CD=21﹣x.在Rt△ABD中,由勾股定理,得AD2=132﹣x2.在Rt△ACD中,由勾股定理,得AD2=202﹣(21﹣x)2.依此列出方程求出x,进一步得到CD的长;
(2)在Rt△ABD中,由勾股定理,得AD的长,再根据三角形面积公式即可求解.
解:(1)设BD=x,则CD=21﹣x,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,由勾股定理,得AD2=AB2﹣BD2,
∴AD2=132﹣x2,
在Rt△ACD中,由勾股定理,得AD2=AC2﹣CD2,
∴AD2=202﹣(21﹣x)2,
∴132﹣x2=202﹣(21﹣x)2,
解得x=5,即BD=5,
∴CD=21﹣x=21﹣5=16;
(2)在Rt△ABD中,
由勾股定理,得AD=![]() =12,
=12,
∴S△ABC=![]() BCAD=
BCAD=![]() ×21×12=126.
×21×12=126.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读完成问题:
数轴上,已知点A、B、C.其中,C为线段AB的中点:
(1)如图,点A表示的数为-1,点B表示的数为3,则线段AB的长为 , C点表示的数为 ;

(2)若点A表示的数为-1,C点表示的数为2,则点B表示的数为 ;
(3)若点A表示的数为t,点B表示的为t+2,则线段AB的长为 ,若C点表示的数为2,则t= ;
(4)点A表示的数为![]() ,点B表示的为
,点B表示的为![]() ,C点位置在-2至3之间(包括边界点),若C点表示的数为
,C点位置在-2至3之间(包括边界点),若C点表示的数为![]() ,则
,则![]() +
+![]() +
+![]() 的最小值为 ,
的最小值为 ,![]() +
+![]() +
+![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律.如:第三行的三个数(1,2,1)恰好对应着![]() 的展开式
的展开式![]() 的系数;第四行的四个数恰好对应着
的系数;第四行的四个数恰好对应着![]() 的展开式
的展开式![]() 的系数;根据数表中前五行的数字所反映的规律,回答:
的系数;根据数表中前五行的数字所反映的规律,回答:
(1)写出图中第六行括号里的数字;(请按从左到右的顺序填写)

(2)求![]() ;
;
(3)利用上面规律计算求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2(2-5)+1=2(-3)+1=-6+1=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( ) 
A.55°
B.60°
C.65°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见下表:

某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x的值和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当n为1,2,3,…时,由大小相同的小正方形组成的图形如图所示,则第10个图形中小正方形的个数总和等于( )
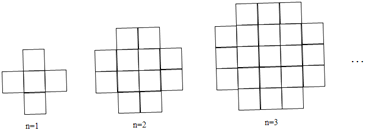
A. 100 B. 96 C. 144 D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com