
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)求∠D的正弦值;
(3)若△ABC外接圆的圆心为P,则点P的坐标为__________.
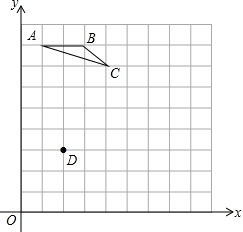
【考点】作图—相似变换;三角形的外接圆与外心.
【分析】(1)根据网格结构,作出DE=2AB,EF=2BC,DF=2AC的三角形即可;
(2)作FG⊥DE于G,在Rt△DFG中利用正弦函数的定义即可求解;
(3)设点P的坐标为(x,y),根据“三角形外接圆的圆心到三角形三个顶点的距离相等”列出等式,化简即可得出点P的坐标.
【解答】解:(1)如下图所示,△DEF即为所求;
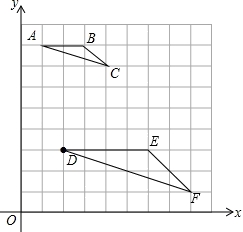
(2)如图,作FG⊥DE于G,
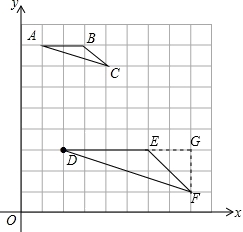
∵在Rt△DFG中,FG=2,DG=6,
∴DF= =
=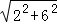 =2
=2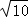 ,
,
∴sin∠D=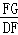 =
=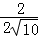 =
=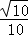 ;
;
(3)设点P的坐标为(x,y);
∵△ABC外接圆的圆心为P,
∴PA=PB=PC,
∵A(1,8),B(3,8),C(4,7),
∴(1﹣x)2+(8﹣y)2=(3﹣x)2+(8﹣y)2=(4﹣x)2+(7﹣y)2,
化简后得x=2,y=6,
因此点P的坐标为(2,6).
故答案为(2,6).
【点评】本题考查了作图﹣相似变换,锐角三角函数的定义,勾股定理,三角形的外接圆与外心,两点间的距离公式,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
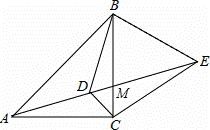
如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.求证:△CBE为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
题面:下列命题说法中:
(1)等腰三角形一定是锐角三角形
(2)等腰三角形有一个外角等于120°,这 一个三角形一定是等边三角形
一个三角形一定是等边三角形
(3)等腰三角形中有一个外角为140°,那么它的底角为70°
(4)等腰三角形是轴对称图形,它有3条对称轴
错误的有( )个
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,
①有一组邻边互相垂直的菱形是正方形
②若2x=3y,则
③若(﹣1,a)、(2,b)是双曲线y= 上的两点,则a>b
上的两点,则a>b
正确的有( )个
A.1 B.2 C.3 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com