
分析 (1)利用已知将各分数分解,进而化简求出答案;
(2)利用已知将各分数分解,进而化简求出答案;
(3)结合(2)中所求,进而分解各数,即可得出答案.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$$+\frac{1}{4×5}$$+\frac{1}{5×6}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$
=1-$\frac{1}{6}$
=$\frac{5}{6}$;
故答案为:$\frac{5}{6}$;
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$;
故答案为:$\frac{n}{n+1}$;
(3)$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$=$\frac{1007}{2015}$,
解得:n=1007.
点评 此题主要考查了分式的加减运算,正确分解各数是解题关键.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答.
要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
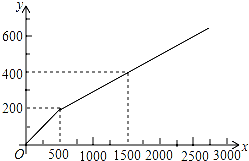 为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.
为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 观察时间 | 10:30(t=0) | 10:36(t=6) | 10:48(t=18) |
| 路牌内容 | 上海90Km | 上海80Km | 上海60Km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com