
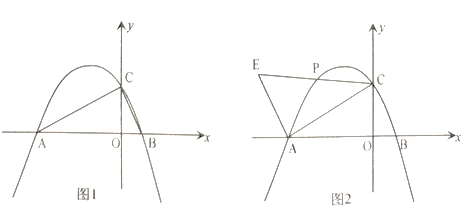
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在符合条件的两点
;(3)存在符合条件的两点![]() ,其横坐标为
,其横坐标为![]() 或
或![]() ;(4)存在符合条件的两点
;(4)存在符合条件的两点![]() 其横坐标为
其横坐标为![]() 或
或![]() .
.
【解析】
(1)令y=0,求解即可得到A、B的坐标;令x=0,即可求得C点坐标,进而得到答案;
(2)先证明 ![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,求出OC的长度,再根据
,求出OC的长度,再根据![]() 不小于90°得到
不小于90°得到![]() 即可求出a的范围;
即可求出a的范围;
(3)在![]() 上取点
上取点![]() 使
使![]() 得到
得到![]() 根据勾股定理求出
根据勾股定理求出![]() 的长, 根据
的长, 根据![]() 得到
得到![]() .再分情况讨论即可得到答案;
.再分情况讨论即可得到答案;
(4)分情况讨论当![]() 得到
得到![]() 再过点
再过点![]() 作
作![]() 轴于点
轴于点![]() 求出点
求出点![]() 的坐标,进而得到P的横坐标,再讨论当
的坐标,进而得到P的横坐标,再讨论当![]() ,类似求解即可得到答案;
,类似求解即可得到答案;
![]() 令
令![]() 得
得![]()
解得![]() ,
,
令![]() 得
得![]() ,
,
![]()
![]() 当
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]() 不小于
不小于![]()
![]()
![]() ,
,
![]()
又![]()
![]()
![]() 存在.当
存在.当![]() 时,
时,
![]()
![]()
![]() ,
,![]()
在![]() 上取点
上取点![]() 如下图,使
如下图,使![]()
则![]()
设![]() 的长为
的长为![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
![]() .
.
①当![]() 时,
时,![]()
![]()
![]()
![]()
过点![]() 作
作![]() 轴于点
轴于点![]()
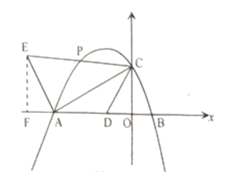
![]() ,
,
![]()
![]()
![]()
![]()
又![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 抛物线解析式为
抛物线解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
②当![]() 时,
时,![]()
![]()
![]()
![]() 时,
时,
同上可得![]() ,直线
,直线![]() 的解析式为
的解析式为![]()
![]()
![]() (舍去),
(舍去),![]() .
.
综上所述,存在符合条件的两点![]()
其横坐标为![]() 或
或![]()
![]() 存在.当
存在.当![]() 时,
时,
![]()
![]()
当![]()
即![]() 时,
时,![]()
过点![]() 作
作![]() 轴于点
轴于点![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
又![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 抛物线解析式为
抛物线解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
当![]() ,
,
即![]() 时,
时,![]()
同上可得![]() ,
,
直线![]() 的解析式为
的解析式为![]()
![]()
![]() (舍去),
(舍去),![]()
综上所述,存在符合条件的两点![]() 其横坐标为
其横坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 和
和![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
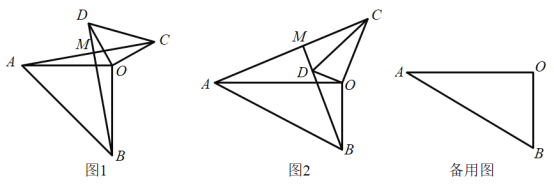
(1)如图1,若![]() ,填空:①
,填空:①![]() 的值为____________;
的值为____________;
②![]() 的度数为___________.
的度数为___________.
(2)如图2,若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示)及
的式子表示)及![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,将三角形
,将三角形![]() 绕着点
绕着点![]() 在平面内旋转,直接写出当点
在平面内旋转,直接写出当点![]() 、
、![]() 、
、![]() 在同一直线上时,线段
在同一直线上时,线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
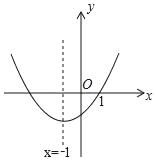
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
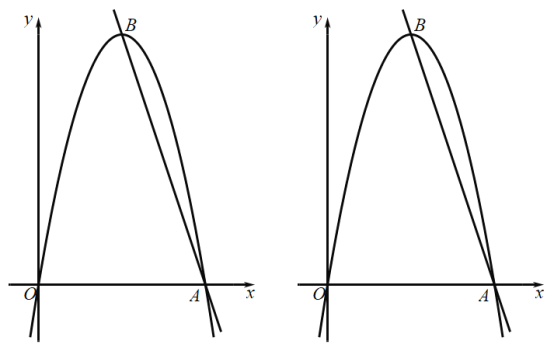
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的正半轴交于点A,抛物线的顶点为B,直线
轴的正半轴交于点A,抛物线的顶点为B,直线![]() 经过A,B两点,且
经过A,B两点,且![]() .
.
(1)求抛物线的解析式
(2)点P在第一象限内对称轴右侧的抛物线上,其横坐标为![]() ,连接OP,交对称轴于点C,过点C作
,连接OP,交对称轴于点C,过点C作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点F,点G是BE的中点,过点G作
于点F,点G是BE的中点,过点G作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 且
且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
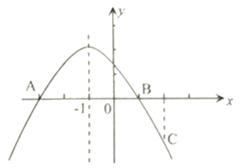
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 点
点![]() ,点
,点![]() 点
点![]() 是抛物线上任意一点,有下列结论:①
是抛物线上任意一点,有下列结论:①![]() ; ②一元二次方程
; ②一元二次方程![]() 的两个根为
的两个根为![]() 和
和![]() ;③若
;③若![]() ,则
,则![]() ;④对于任意实数
;④对于任意实数![]()
![]() 总成立.其中正确结论的个数为 ( )
总成立.其中正确结论的个数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校每个年级学生刚好为500人,为了解数学史知识的普及情况,随机从每个年级各抽10名学生进行测试,测试成绩整理如下:
年级 | 学生测试成绩表 | |||||||||
七年级 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年级 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年级 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求每个年级恰好都有一名学生参加的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校按照开展“阳光体育运动”的要求,决定主要开设![]() :乒乓球、
:乒乓球、![]() :篮球、
:篮球、![]() :跑步
:跑步![]() :跳绳这四种运动项目.为了了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
:跳绳这四种运动项目.为了了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
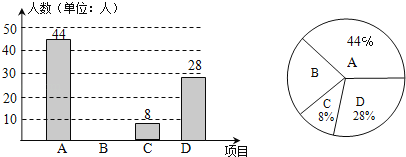
(1)样本中喜欢![]() 项目的人数百分比是多少?其所在扇形统计图中的圆心角的度数是多少?
项目的人数百分比是多少?其所在扇形统计图中的圆心角的度数是多少?
(2)把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630
查看答案和解析>>
科目:初中数学 来源: 题型:
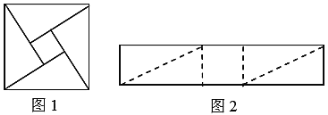
【题目】如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com