
【题目】某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
螺丝 | a | 1.0 | 2.0 |
螺母 | a﹣0.3 | 0.6 | 2.0 |
(1)已知用50元购进螺丝的数量与用20元购进螺母的数量相同,求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个.
①该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?(用含a的代数式表示)
②由于原材料价格上涨,每个螺丝和螺母的进价都上涨了0.1元.按照①中的最佳进货方案,在销售价不变的情况下,全部售出后,所得利润比①少了260元,请问本次成套的销售量为多少?

【答案】(1)a=0.5;(2)①购进螺丝700个,购进螺母2300,利润为2700-3000a;②成套的销售量为150套
【解析】分析:(1)根据用50元购进螺丝的数量与用20元购进螺母的数量相同找出等量关系列方程求解,解分式方程要验根;
(2)①设购进螺丝x个,则购进螺母(3x+200)个,根据两种配件的总量不超过3000个列不等式求出x的取值范围;然后根据总利润=成套卖的利润+单卖螺丝的利润+单卖螺母的利润列出一次函数关系式求解;②设成套的销售量为m套,则零售的螺丝为(700﹣m)个,零售的螺母为(2300﹣2m)个,结合①中求得最大利润列方程求解.
详解:(1)依题意得![]() a=0.5,
a=0.5,
经检验:a=0.5是原方程的解,且符合题意.
(2)①设购进螺丝x个,则购进螺母(3x+200)个,依题意得
x+(3x+200)≤3000,
x≤700,
则成套的卖出时利润为:![]() x[2﹣a﹣2(a﹣0.3)]元;单个螺丝的利润为:
x[2﹣a﹣2(a﹣0.3)]元;单个螺丝的利润为:![]() x(1﹣a);
x(1﹣a);
单个螺母的利润为:(3x+200﹣x)[0.6﹣(a﹣0.3)],
设利润为y元,则![]() ,
,
=(3.6﹣4a)x+(180﹣200a).
解法一:
由已知得![]() ,
,
解得a<0.9.
∵当a<0.9时,k=3.6﹣4a>0,
∴函数y=(3.6﹣4a)x+(180﹣200a)中的y随x增大而增大.
∴当x=700时,y最大=2700﹣3000a.
解法二:
分两种情况讨论:
当3.6﹣4a>0,即a<0.9时,函数y=(3.6﹣4a)x+(180﹣200a)中的y随x增大而增大.
∴当x=700时,y最大=2700﹣3000a,
当3.6﹣4a≤0时,a≥0.9.
∵根据成套销售价应高于成本价可得:a+2(a﹣0.3)≤2,即a≤![]() ,
,
∴此时不符合题意,舍去.
②设成套的销售量为m套,则零售的螺丝为(700﹣m)个,零售的螺母为(2300﹣2m)个,依题意得:
m[2﹣a﹣2(a﹣0.3)﹣0.3]+(700﹣m)(1﹣a﹣0.1)+(2300﹣2m)[0.6﹣(a﹣0.3)﹣0.1]=﹣0.2m﹣3000a+2470,
故:﹣0.2m﹣3000a+2470=2700﹣3000a﹣260,
解得:m=150,
故成套的销售量为150套.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
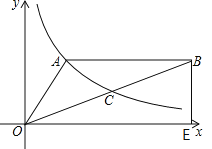
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.

(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一边靠墙,其他三边用12米长的篱笆围成一个矩形(ABCD)花圃.

(1)如果设花圃靠墙的一边的长为x(米).花圃的面积为y(平方米),求x,y满足的关系式;
(2)当长x从4米变到6米时,面积y变化如何?
(3)当长x从6米变到8米时,面积y变化如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
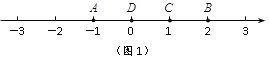
知识运用:
⑴ 如图1,点B是(D,C)的好点吗? (填是或不是);
⑵ 如图2,A、B为数轴上两点,点A所表示的数为-40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
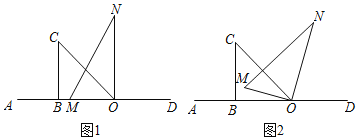
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A、B两种型号的健身器材时,共有多少种组装方案?
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com