练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个正方形和两个等边三角形的位置如图所示，若∠1=50°，则∠2+∠3=（　　）

    A.190°
    B.130°
    C.100°
    D.80°

    【答案】C
    【解析】解：如图，∠BAC=180°﹣90°﹣∠1=90°﹣∠1，
    ∠ABC=180°﹣60°﹣∠3=120°﹣∠3，
    ∠ACB=180°﹣60°﹣∠2=120°﹣∠2，
    在△ABC中，∠BAC+∠ABC+∠ACB=180°，
    ∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°，
    ∴∠1+∠2=150°﹣∠3，
    ∵∠1=50°，
    ∴∠2+∠3=150°﹣50°=100°．
    故选C．

    设围成的小三角形为△ABC，分别用∠1、∠2、∠3表示出△ABC的三个内角，再利用三角形的内角和等于180°列式整理即可得解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】随着互联网、移动终端的迅速发展，数字化阅读越来越普及，公交上的“低头族”越来越多．某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查（如图1），并将调查结果绘制成图2和图3所示的统计图（均不完整）．

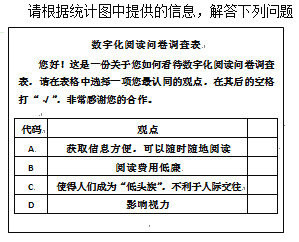
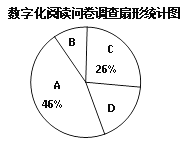
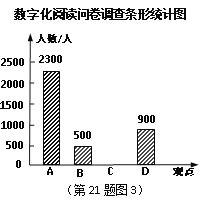
    （1）求出本次接受调查的总人数，并将条形统计图补充完整；

    （2）表示观点B的扇形的圆心角度数为 度；

    （3）若嘉兴市人口总数约为270万，请根据图中信息，估计湖州市民认同观点D的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程或方程组
    （1）4（2﹣x）2=9
    （2） ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形中，∠1与∠2不是同位角的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知对任意有理数a、b，关于x、y的二元一次方程（a﹣b）x﹣（a+b）y=a+b有一组公共解，则公共解为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把一元二次方程x2+6x-1=0通过配方化成(x+m)2= n的形式为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，已知AB＝8cm，BC＝10cm，折叠矩形的一边AD ， 使点D落在BC边的中点F处，折痕为AE ， 求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线

    (1)若抛物线的顶点坐标为(2，－3)，求b，c的值；

    (2)若，是否存在实数x，使得相应的y的值为1，请说明理由；

    (3)若且抛物线在－2≤x≤2上的最小值是－3，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时，有-1 ≤ y1 - y2 ≤ 1成立，则称这两个函数在a ≤ x ≤ b上是“相邻函数”，否则称它们在a ≤ x ≤ b上是“非相邻函数”.

    例如，点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点，当-3 ≤ x ≤ -1时，y1 - y2 = (3x + 1) - (2x - 1) = x + 2，通过构造函数y = x + 2并研究该函数在-3 ≤ x ≤ -1上的性质，得到该函数值的范围是-1 ≤ y ≤ 1，所以-1 ≤ y1 - y2 ≤ 1成立，因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.

    （1）判断函数y = 3x + 2与y = 2x + 1在－2 ≤ x≤ 0上是否为“相邻函数”，说明理由；

    （2）若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”，求a的取值范围；

    （3）若函数y =与y =－2x + 4在1 ≤ x ≤ 2上是“相邻函数”，直接写出a的最大值与最小值.

    查看答案和解析>>

    同步练习册答案